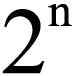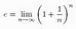素因数分解、累乗数が好き！コミュの【ベースキャンプ２】累乗数

累乗数とは、他の自然数の累乗になっている自然数のことで、mのk乗（m, kは自然数でk≧2）の形の数です（m^kで表します）。

累乗数について、他のトピが立つまでは何でもここに書きましょう。
→話題が盛り上がったら、トピを独立させていきましょう。

ここから派生したトピを掲げておきます↓
http://mixi.jp/view_bbs.pl?id=10316247&comm_id=1265663

******************************************************
出題と解答状況です。
トピ読みのナビにしてください。

【問1】（出題）No.4：幹事長（勧進帳）さん

コメント(61)

最初
全て
最新の40件

前

[22] mixiユーザー 03月06日 09:14

いまさら移動するとややこしいので（笑）、このネタはこのトピで続けましょう。
いずれ「コミュ内のネタ一覧トピ」を作るつもりですので、その際にここにあることを説明します。

>19
標準漢字環境に配慮して、一部かな表記にされたのかな？
標準的でないかも知れませんが、フルバージョンで出しておきます。
文字化けしたらご容赦ください。

12無量大数3456不可思議7891那由他2345阿僧祇6789恒河沙1234極5678載9123正4567澗8912溝3456穰7891秭2345垓6789京1234兆5678億9123万4567

[23] mixiユーザー 03月06日 09:57

"じょ"は漢字を覚えてなかったし、たしか難しい字だったと思うので平仮名にしておきました。

[24] mixiユーザー 03月13日 07:45

累乗を用いた方程式に関する問題

p^p * q^q = r^r
を満たす非自明なp,qおよびrの組を見つけてください。

非自明というのは、誰の目にも明らかなp=q=r=1という
ような場合は除く、ということです。

これは見かけの割りにかなり難しい問題だと思います。

[25] mixiユーザー 03月17日 06:08

>24の回答というか、トリビア的な話として。

方程式p^p*q^q=r^rを満たす非自明なp,q,rの組み合わせ
として知られている最小は
p = 2985984 (=12^6)
q = 1679616 (=6^8)
r = 4478976 (=2^11*3^7)

ということが私の持っている本に紹介されています。

[26] mixiユーザー 03月17日 09:45

↑おもしろいネタ！

このベースキャンプが久々ににぎわってきました。

[27] mixiユーザー 03月17日 20:38

一般解はどうやって求めるんですか？

[28] mixiユーザー 03月18日 04:46

書き込み24に対する自明な解

それはpまたはqが1であることが自明解であることは分かります。

それ以外は全て非自明解だと思いますが、（それ以外に
自明な解があるよ！という突っ込み歓迎です！）
一筋縄ではそれらは見つけられないのではないかと思います。
ただ、25の書き込んだ最小解を計算で確かに合っている
ことを確認しながら思ったのですが、（紙と鉛筆があれば
確認できます）解をみつけるには

(1)p,q,rが全て共通した素因数を持つこと

(2)rを素因数分解したときの指数、25の例では7と11ですが、
これがp,q,rを構成する素因数の累乗和で表すことができる
例えば、
7=2^2+3^1
11=2^3+3^1または2^1+3^2

この条件で絞り込めば、他の非自明な解を見つけることも
できるのでは？と思っています。
皆さんでも色々考えてみませんか？

[29] mixiユーザー 03月25日 06:51

少ない種類の数で構成される平方数

11^2=121, 26^2=676のように
（これらの例では2種類ですが）少ない種類の数で構成される
平方数にはどんなものがあるだろうか、無限に存在するだろうか？という問題があります。

ただし、この問題では0を含まない場合に限定します。
そうしないと(10^n)^2を考えれば無限に自明解が存在するからです。
4^2=16, 5^2=25,....
に始まり
19個目の解が264^2=69696
20個目の解が3114^2=9696996
そして
21個目の解が81619^2=6661661161
が知られていますが、
現時点でこれ以降の解は知られていません。

なお、1種類の数字からなる平方数が存在しないことは
比較的簡単に証明できます。

[30] mixiユーザー 03月25日 12:21

>29
なるほど。

自然数遊び系の問題には
○狭義の自然数遊び（記数法の影響を受けない）
○広義の自然数遊び（記数法の影響を許す）
の2種類があると思います。

これは後者の中で基本的な問題ですね。

＞少ない種類の数で構成される平方数

これは、どうでしょう。。
上の事情から、
「十進法において少ない種類の数で表記される平方数」
と表現するのがよいかと。

●
さて、累乗数キリ番で19個目の解に至ると、人にも喜ばれそう。。
いま半分近くまで来ているので、引き続きこれを楽しみに、累乗数キリ番を続けます。

ちなみに私は、「十進法において高々2種類の数で表記される累乗数」の中では
6^5=7776
が好きです。

[31] mixiユーザー 03月26日 03:58

>binjiさん

>「十進法において少ない種類の数で表記される平方数」
>と表現するのがよいかと。

そうですね。
自分は特に断りを入れない場合は10進数表現である、
という感覚であり、あまり厳密に書かないほうが一般受け
しやすいと言う判断で当初の表現にしたのですが、
厳密には言われるとおりです。

なお、3乗以上の場合は更に限られた場合しか解が知られていません。
6^5は稀有な存在です。

[32] mixiユーザー 03月26日 08:53

＞あまり厳密に書かないほうが一般受けしやすい

そういう姿勢で、結構です！
私が妙にこだわるのは、累乗数キリ番をやっているための個人的事情ですね。

「なんでこれのキリがいいんだ？」と受け止められることがあり、「記数法の影響を排除してキリ番を選んだら、こうなるでしょう」と反論することが多いので。

管理人として特に注文、という意味合いはありませんので、気にしなくてよいです。

[33] mixiユーザー 03月28日 03:55

>binjiさん
はは、それではお言葉に甘えて
整数の逆順加算という問題をご存知でしょうか。

10進数で表した自然数について、その数を逆に並べた自然数を
元の自分自身に加える。この操作を繰り返すと、有限回で回文的な
自然数になる、という予想があります。
回文的というのは最初から読んでも、最後から読んでも同じ数になる、
ということです。

例えば19を例に取ると
19 + 91 = 110
110 + 011 = 121
2回の操作で回文的になります。
小さな整数で確認してみると、いくつかのステップの後に
回文整数になることが確認できます。
89では少し苦労すると思います。
どんな自然数でも同じ操作を繰り返すと、回文的な整数にたどり着くか？
という問題が、「自然数の加法回文性」という問題です。

とはいうものの、196でスタートした場合、現時点で
数億ステップまで計算されているのですが、
回文整数に到達していないそうです。
これに限らず、実は大きな整数をスタートにした場合、
寧ろ回文的になってくれるほうがまれで、なかなか
回文的にならないことが分かってきています。
それでいながら、絶対に回文整数にならない、と
判明している数も知られていません。
ただし、これは10進数の場合で2進数の場合には
同様の操作によって回文的にならない反例の存在が
知られています。

[34] mixiユーザー 03月28日 13:40

回文性について、

繰り上がりがなければ、必ず回文的になります。繰り上がりがあれば回文的にはならないはず。
ということは、数字を逆にして足して繰上りがなければ、この手続きを終了することになるのか。

ちなみに、ベースキャンプ１の１９番あたりに、累乗回文和等式（だったかな？）というのが出てきました。一度こちらも御覧になってみてはいかがでしょう。

[35] mixiユーザー 06月25日 12:17

「212の2乗」という累乗数キリ番を差し上げていて思ったのだけど、この累乗の計算をふつうの筆算でやるｔ、一度も繰り上がりがなくてきれいです。

それで、元の数が3桁回文であることが遺伝して、きちんと5桁回文になってくれます。
なんだかうれしくなりました。

[36] mixiユーザー 08月09日 12:43

＞29
＞少ない種類の数で構成される平方数

次のキリ番が、235^2=55,225になりました。
達成時に、特集日記をやろうかな

[37] mixiユーザー 11月10日 15:40

「４種類の形で累乗数になる数」は、「５種類の形で累乗数になる数」よりもレアですね。

そんなことを、累乗数キリ番日記を書いていて思いました

<人生で実質最レアのキリ番。>（足跡数65,536件のキリ番）
http://mixi.jp/view_diary.pl?id=615777602&owner_id=5383118
<人生で実質最高のキリ番。> （足跡数4,096件のキリ番）
http://mixi.jp/view_diary.pl?id=221128041&owner_id=5383118

[38] mixiユーザー 04月07日 01:39

530万以上540万未満の自然数（10万個）を対象に、累乗数の存在状況を調べたことがあります。

すると、
○平方数21個
○立方数1個
○4乗数1個
○純計22個
でした。

漠然とイメージしていたより、少なかったです。
累乗数の密度はこんなものなのか、と実感を持つことができました。

※関係トピ

http://mixi.jp/view_bbs.pl?id=28336548&comm_id=1808352

[39] mixiユーザー 09月16日 01:54

累乗数キリ番も5桁になってからは、暗算力も大してないので大変。
にわかになるほどとは思えない数が、多く続きました

しかし5桁の終盤になって、わかりやすい数が続いています。
たとえば次は、94864です；

94864
＝9000＋4800＋64
＝300^2＋2*300*8＋8^2
＝(300＋8）^2
＝308^2.

というわけで、この辺は規則的で助かっています

[40] mixiユーザー 10月16日 00:04

平方数9と立方数8は、わずか1違いの、近い「平方数・立方数ペア」です。
25と27も近いですね。

このような「平方数・立方数ペア」の近さを、比を指標として考えてみました。
m^2とn^3の近さを、次の関数で表します；
f(m,n)=n^3/|m^2-n^3|.
たとえばf(3,2)=8/|9-8|=8.

小さいほうから順に見て、新記録を達成するたび記録してみました。
小数点以下四捨五入で；
f(3,2)=8.
f(5,3)=14.
f(11,5)=31.
f(32,10)=42.
f(42,12)=48.
f(47,13)=183.
f(58,15)=307.
f(70,17)=378.
f(148,28)=457.
f(156,29)=460.
f(181,32)=4681.
f(253,40)=7111.
f(312,46)=12167.
f(985,99)=13112.

この分布に、意味があるのかどうか存じません。

累乗数キリ番をしていて、
○32,761＝181^2と32,768＝32^3
○64,000＝40^3と64,009＝253^2
○97,336＝46^3と97,344＝312^2
が近くておもしろかったので、取り上げてみた次第です

[41] mixiユーザー 11月16日 01:19

>39
自己レスですが、6桁となると、わかりやすい累乗数はさらにレアになります。

ほぼ自明なものから順に、タイプ別に並べます；

100000

160000
250000
360000
490000
640000
810000

125000
216000
343000
512000
729000

168100

160801
251001
361201
491401
641601
811801
161604
252004
362404
492804
643204
813604
162409
253009
363609
494209
644809
815409
163216
254016
364816
495616
646416
817216
164025
255025
366025
497025
648025
819025
164836
256036
367236
498436
649636
165649
257049
368449
499849
166464
258064
369664
167281
259081

以上です。
ほかにいいのがありましたら、教えてください。

[42] mixiユーザー 03月07日 01:46

累乗数キリ番は、6桁序盤の砂漠（上記コメント41のような分かりやすさがない）をさまよっています。
しかし、小さな発見がありました。

32^2=1024.
33^2=1089.
34^2=1156.
35^2=1225.
なのですが、

332^2=110224.
333^2=110889.
334^2=111556.
335^2=112225.

いやあ、エコーがかかったみたいですねえ

[43] mixiユーザー 03月07日 05:38

二桁の数で他にこのような性質を持つ数を調べてみたところ、
10の倍数を除くと
65^2 = 4225 ; 665^2 = 442225
66^2 = 4356 ; 666^2 = 443556
67^2 = 4489 ; 667^2 = 444889
68^2 = 4624 ; 668^2 = 446224
95^2 = 9025 ; 995^2 = 990025
97^2 = 9409 ; 997^2 = 994009
98^2 = 9604 ; 998^2 = 996004
99^2 = 9801 ; 999^2 = 998001

と、合計12個あることがわかりました。
意外と多いようです。

この表からもれた96は
96^2=9216 に対し996^2 = 992016
となり、微妙にエコーしています。
また、この見つかった数の周辺には
こういったエコーにノイズが含まれているものがいくつか見つかりました。

今回,ab^2 = cdef に対して、
aab^2 = ccdeefとなる形のものがほとんどですが、
95だけが aab^2 = ccddef となり、例外的です。

95以外の数はすべていくつか連続しており、
最初に発見された数の2倍,3倍に近いようです。

[44] mixiユーザー 03月07日 13:56

おもしろくなってきました

[45] mixiユーザー 03月29日 21:56

僕の日記のネタから

555555555555×555555555555＝555555555555^2

を紙と鉛筆で素早く正確に計算する方法を考えてください。

ヒント：5がn個のn桁の場合、足し算を高々n回すれば良いはずです。

[46] mixiユーザー 03月29日 22:44

11×11=121, 111×111=12321, 1111×1111=1234321 と同様に考えると
111111111111×111111111111 は 12345679012320987654321 とわかります。
（12345678901210987654321+111110000000000 と繰り上がりを分けて考えると簡単かも）
これに0を2つ加えて2回半分にすれば
1234567901232098765432100
→617283950616049382716050
→308641975308024691358025
と求まりますね。

[47] mixiユーザー 03月30日 00:37

＞らすかるさん

なるほど、その路線ですか^^;　僕の想定外でしたよ。
大きな数の掛け算が１回出て来ますね。

(10a+5)^2=(a*a+a)*100+25

を使うと、足し算の連続で計算できます。

[48] mixiユーザー 03月31日 15:24

なるほど

5555...5555*5555...5555が,

308641975
308641975
....
308...
...135
802469135
802469135
....
8025

といった形になるのも111....1同士の掛け算からわかりますね。

[49] mixiユーザー 04月01日 13:35

5が連続する自然数の２乗を連続足し算でやってみます。

25----->5^2
+5
--
30----->5^2+5
3025----->55^2=(5^2+5)*100+25
++55
----
3080----->55^2+55
308025----->555^2=(55^2+55)*100+25
+++555
------
308580----->555^2+555
30858025----->5555^2=(555^2+555)*100+25
++++5555
--------
30863580----->5555^2+5555
3086358025----->55555^2=(5555^2+5555)*100+25
+++++55555
----------
3086413580----->55555^2+55555
308641358025----->555555^2=(55555^2+55555)*100+25

足し算の桁数が増えて行くだけで、あとは繰り返しです。

[50] mixiユーザー 09月11日 00:18

9月4日（月も日も平方数ですね）に放送された高校生クイズ全国大会の準決勝延長戦で、
「サイコロを6回投げて、その間に目の合計数が6となる確率を求めよ。」
という趣旨の問題が出題されました。

分母が6の累乗となることは、サイコロ確率問題では定番ですが、興味深かったのは分子のほうです。
地上波人気番組で、2や6以外の数の累乗で、あんなに大きな数が見られるとは思いませんでしたねえ。。

もっとも、視聴者のうちで、あの分子が累乗数だと気付いた人は少ないかもしれません。
この問題はネット上で話題になりましたが、「大した難問ではない、テレビ局は演出しすぎだ」と説くコメントが多く、分子の5桁の数について性質を説明するコメントはほとんど見かけませんでした。

確率問題ですから、解法はたくさんあることでしょう。
日記で、自分なりに気に入った解法を取り上げました

http://mixi.jp/view_diary.pl?id=1277492635&owner_id=5383118

[51] mixiユーザー 12月16日 01:01

6桁の累乗数キリ番が、16万台に入っています。
コメントNo.41で見ましたように、わかりやすい平方数が多くて、にやけています

[53] mixiユーザー 01月07日 01:03

あけましておめでとう、ことしもよろしく。
（累乗数トピで申し上げるのも変ですが。）

キリ番進行の関係で、また6桁累乗数のお話です。

164025=405^2ですが、これは、
○「164025」の中に、「405」という数字が隠れている。
というふうに見えました。

このように、「元の数の各桁が、並び方も維持したまま、その累乗数の一部として表れる」ことは、けっこうめずらしいように思いました。
特に、元の数が3桁ともなると。。

どなたか、めずらしさを評価していただけるとありがたいです。

[54] mixiユーザー 01月08日 17:46

あけましておめでとうございます。
お久しぶりです。

早速1億まで調べてみました。
まず、平方数の一部にそっくりそのまま同じ数字が現れるものについて。

ただし、下k桁が元の数になる物について(6,7109376など)
6^2 = 36より60^2 = 3600も満たすといった例があるので、
ここでは10の倍数は除きました。

1 1
5 25
6 36
25 625
76 5776
376 141376
625 390625
3792 14379264
9376 87909376
14651 214651801
90625 8212890625
109376 11963109376
495475 245495475625
505025 255050250625
890625 793212890625
971582 943971582724
1713526 2936171352676
2890625 8355712890625
4115964 16941159649296
5133355 26351333556025
6933808 48077693380864
7109376 50543227109376
10050125 101005012515625
12890625 166168212890625
48588526 2360844858852676
50050025 2505005002500625
66952741 4482669527413081
87109376 7588043387109376
88027284 7748802728416656
88819024 7888819024312576

下k桁が同じになる例では
5,25,625,90625,
6,76,376,9376...と何か規則的な感じになっており、
途中が同じになる時も何か面白そうな並びだったりしますが、こんな感じです。

[55] mixiユーザー 01月08日 17:55

次に条件の「この順で現れる」について
上のpostの結果も含みます。
1,000^2 = 1,000,000以下について

1 1
5 25
6 36
11 121
25 625
76 5776
95 9025
96 9216
101 10201
105 11025
125 15625
205 42025
305 93025
371 137641
376 141376
405 164025
441 194481
501 251001
505 255025
506 256036
525 275625
601 361201
605 366025
625 390625
676 456976
705 497025
756 571536
805 648025
825 680625
826 682276
905 819025
946 894916
976 952576
995 990025
996 992016

[56] mixiユーザー 01月08日 18:06

以下、nまでの条件を満たす数の個数kについての"n k"です。

10の倍数を除いたとき
10 3
100 8
1000 35
10000 130
100000 512
1000000 1897
10000000 7252
100000000 27688

10の倍数を含めたとき (0を含む)
10 4
100 12
1000 47
10000 177
100000 689
1000000 2586
10000000 9838
100000000 37526

といった感じでした。桁数が上がるほどレア度は上がるのですね。

[57] mixiユーザー 01月08日 18:39

> 10 4
0,1,5,6,10 の5個では？
「0を含む」はそういう意味ではないのかな？

[58] mixiユーザー 01月08日 21:46

>らすかるさん
n未満の数についてでした...。

[59] mixiユーザー 01月09日 01:28

n未満なら了解です。
ちなみにもう一つ先は
1000000000 144721
（10の倍数を含めない場合は144721-37526=107195）
となりました。
10^n未満の個数は 3.75^n (もしくは (10^n)^0.574)個あたりに
収束しそうな雰囲気ですね。

[60] mixiユーザー 01月09日 04:24

細＠わんどさん、らすかるさん、さっそくにありがとうございます。
例によって定義があいまいなままお願いしましたのに、定義も明確化しながらご検討いただき、お世話になりました。。

コメントNo.54)
＞下k桁が同じになる例では
＞5,25,625,90625,
＞6,76,376,9376...と何か規則的な感じになっており、

そうですね。
25や76を平方して「おや？」と感じたことがある人は多いと思います。
その先についての興味もありました。

コメントNo.55)

3桁の数のうち下2桁の形から必ずこの仲間になるのは、「x00」「x05」に限られることも確認できました。

こういう分布は、n進法の「n」に依存するのだろうと思いますが、

コメントNo.59)
＞10^n未満の個数は 3.75^n (もしくは (10^n)^0.574)個あたりに収束しそうな雰囲気ですね。

味わい深いですね。
（生物としての偶然から）10という合成数を使って位取りをしていることのめぐりあわせを、改めて感じました。

[61] mixiユーザー 01月09日 13:09

上記「x05」タイプにつきまして。
私は近年、演算力が落ちています。
そこで、しかたないのでむかしの自分を使います。

コメントNo.9)
(10n+5)^2=(10n)^2+2(10n)*5+5^2=100n(n+1)+25.

と、4年あまり前に書きましたが、これを応用します；

(100n+5)^2=(100n)^2+2(100n)*5+5^2=10000n^2+(1000n+25).

3桁の数(100n+5)を平方すると、下4桁に必ず(1000n+25)が現れますね。
ですから、3桁レベルでの「x05」タイプ発生は、当然と言えば当然でした。
そして、nが大きいときの(100n+5)については、あまり役に立ってくれないことにも気づきました。。

ログインすると、残り22件のコメントが見れるよ