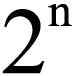素因数分解、累乗数が好き！コミュの【ベースキャンプ５】整数ネタ・ジュニア

メンバーも増えました。
このコミュに参加しやすいよう、簡単な整数問題など出し合いましょう。

このジュニア版では、出題後、答案提出保留時間は設けません。
すぐに答えていただいて結構です。
※交流のためのトピですから、解答の他、併せて問題への印象など書いていただけるとありがたいです。

参加したくなりそうな人は、まず自己紹介を済ませておいて！

●
なお、証明を要するタイプの出題ネタや、出題者も正解に至っていない課題の提供は、ここではなく、姉妹トピ「【ベースキャンプ３】整数ネタ・シニア」にお願いします。

******************************************************
出題と解答状況です。
トピ読みのナビにしてください。

【問1】（出題）No.1：まこぴ～さん、（正解）No.12：binji 、No.16：まこぴ～さん、No.20：binji
【問2】（出題）No.2：にゃーさんさん、（正解）No.11：にゃーさんさん
【問3】（出題）No.22：まこぴ～さん、（正解）No.29：よってぃーさん、No.30：まこぴ～さん
【問3-2】（出題）No.32：まこぴ～さん、（正解）No.33：よってぃーさん、No.36：まこぴ～さん
【問4】（出題）No.37：パルキーさん、（正解）No.39：パルキーさん
【問5】（出題）No.40：にゃーさんさん、（正解）No.42：愛さん
【問6】（出題）No.49：にゃーさんさん、（正解）No.54：にゃーさんさん
【問7】（出題）No.55：binji、（正解）No.56：漢字練習帳さん
【問8】（出題）No.57：binji、（正解）No.58：binji、(関連）No.59：まこぴ～さん
【問9】（出題）No.63：パルキーさん
（以降、未整理）

コメント(86)

最初
全て
最新の40件

前

[47] mixiユーザー 05月28日 15:02

>45
ご苦労様でした！

＞平面内での領域の形が結構きれいですょ
日記では、簡単な文章だけでしたね。
気になっていますが！

＞対数化して倍精度型にするとか。
何か手筋があると思いましたが、私が言いたかったことはこれに近そう（イメージだけど

>46
解明ありがとう。

＞10/log10
＞4.342945
＞108.3673102
こういう世界の中の、物語だったのですね。

今度はf(m,n)=m^n/n^mとか、g(n)=n/lognが何をしてくれるんだか、気になりますね！

[48] mixiユーザー 06月06日 08:30

g(n)=n/logn～π(n)　が見えますね。π(n)はn以下の素数の数ですが＾＾；

[49] mixiユーザー 09月22日 10:08

全く別の問題を考えてたら思いついた問題を出してみます☆

**********

数列
0,0,1,1,2,3,4,5,7,8,10,12,14,16,19,…

の30番目の数は何でしょう？

**********

[50] mixiユーザー 09月27日 11:53

昔はこういうの好きだったんですけどね。
今や発想力がなくなってます。

なんとなくフィボナッチ数列が関連してると思うんですが…

[51] mixiユーザー 09月27日 12:48

答えはわかったのですが、簡単ではなかったです＞＜

[52] mixiユーザー 09月27日 15:45

ぉ

わかった人が出ましたね～♪

ちなみに、ヒントは「輪唱」です☆

[53] mixiユーザー 09月28日 01:03

↑遅くなりましたが、トピ説明に出題登録しておきました。
解いた方、出題者の方、適当なところで答をお願いします。

[54] mixiユーザー 09月28日 07:23

49:
じゃあ、出題して１週間近く経ったので、そろそろ種明かしを。。

答えから先に言うと、30番目は
75
です。

この数列は、
0=0
0=0
1=1
1=1
2=2
3=2+1
4=3+1
5=3+2
7=4+2+1
8=4+3+1
10=5+3+2
12=5+4+2+1
…

という感じで、同じ数字を２回ずつ使いながら１ずつ増やしていき、かつ、３つごとに加える項の数を増やして１から足しています。
（これを自分は「輪唱」って言いました。）

30番目だと、
14+13+11+10+8+7+5+4+2+1=75

というわけです。

…さて、こんな怪しい数列ですが、実は全く別の意味を持っています。

それは…
「ｎ番目の自然数を３つの自然数の和として表すときの組み合わせの数の数列」
というもの。

例えば、
n=5
であれば、
5
=1+1+3
=1+2+2
で２通り。
つまり、数列の５番目は２。

n=10
のときは、
10
=1+1+8
=1+2+7
=1+3+6
=1+4+5
=2+2+6
=2+3+5
=2+4+4
=3+3+4
の８通りなので、数列の１０番目は８。
といった感じ。

で、最初に書いた「輪唱」の各項は、このときの１つめの項が同じ組み合わせの数を表しています。

もっと言うと、なんで「３整数の和」に分解したのか、と言うと、実はこれ、
「何人かでじゃんけんをしたとき、『ぐーちょきぱー』であいこになるときの、同じ手の人の数の組み合わせ」
を考えていたときに思いついたからです☆

５人でじゃんけんして、
ぐー、ぐー、ちょき、ぱー、ぱー
だったら、人数は
２人、１人、２人。

並び替えて
５＝１＋２＋２

こんなところから生まれた数列でした☆

[55] mixiユーザー 01月04日 01:41

新年第1問！

2つの数字を合計20個掛け合わせて、なるべく約数が多い数を作ります。
次の各組について、前者の数字を何個使ったらよいでしょうか。
またそのとき、約数は何個になりますか。

簡単な順に並べていますので、できるところまでやってみませんか。
答だけ出してくれたらよいですよ！

（例）2と3.　　　　　　→（答）10個、121個。（対称性から、これは直感的にできそうですね。）

(1)3と8.
(2)4と6.
(3)6と8.
(4)5と6.

[56] mixiユーザー 01月09日 01:08

漢字練習帳さんからいただいた解答です。
（【ベースキャンプ３】No.138に詳しい説明が。）
**************************************
解答：（前者の個数，後者の個数，約数の個数を記します）
(1)3：10個，8：10個，約数：341個
(2)4：0個，6：20個，約数：441個
(3)6：15個，8：5個，約数：496個
(4)5：6個，6：14個，約数：1575個
**************************************
正解です！

[57] mixiユーザー 03月03日 01:43

自然数を「連続する自然数の和」で表す方法の数は、その自然数の奇数である約数の数に等しいです。
（【ベースキャンプ３】No.186～191ご参照。）

例です。

自然数を「連続する自然数の和」で表す方法の数が2個以上ある最小の数は、3です。
3=3.
3=1+2.

自然数を「連続する自然数の和」で表す方法の数が3個以上ある最小の数は、9です。
9=9.
9=4+5.
9=2+3+4.

ここから、問題です。

(1)自然数を「連続する自然数の和」で表す方法の数が10個以上ある最小の数は、何ですか。
その方法も、そのまま列挙してください。

(2)自然数を「連続する自然数の和」で表す方法の数が20個以上ある最小の数は、何ですか。

[58] mixiユーザー 03月06日 00:14

No.57の答です。

(1)
315=3^2*5*7です。

その方法は、以下の12個です；
315=315.
315=104+105+106.
315=31+32+33+34+35+36+37+38+39.
315=61+62+63+64+65.
315=14+15+16+17+18+19+20+21+22+23+24+25+26+27+28.
315=16+17+18+19+20+21+22+23+24+25+26+27+28+29.
315=42+43+44+45+46+47+48.
315=5+6+7+8+9+10+11+12+13+14+15+16+17+18+19+20+21+22+23+24+25.
315=27+28+29+30+31+32+33+34+35+36.
315=9+10+11+12+13+14+15+16+17+18+19+20+21+22+23+24+25+27.
315=50+51+52+53+54+55.
315=157+158.

(2)
2835=3^4*5*7です。

その方法は、20個です。

[59] mixiユーザー 03月06日 12:48

「連続する自然数の和」で表現可能な自然数は、

s=?[i=1 to k](n+i)=(2n+k+1)*k/2

で、sの約数の個数だけ解があるという考え方ですね。

[60] mixiユーザー 03月06日 23:58

>59

「連続する自然数の和」で表現可能な自然数は、
（【ベースキャンプ３】No.191で論じたとおり、）
「その数の奇数である約数の個数だけ解がある」
というところまでたどりつきました。

上記のsは、それと見かけが違いますが、同値なのでしょうか？
イメージがわいていませんので、解説いただけると助かります。

[61] mixiユーザー 03月07日 21:29

[上記のsは、それと見かけが違いますが、同値なのでしょうか？]

s=(2n+k+1)*k/2、あるいは、2s=(2n+k+1)*k

において、右辺の「(2n+k+1)とkは必ず偶数と奇数となる」という解説でよろしいでしょうか？

[62] mixiユーザー 03月07日 21:40

忘れてました。

後は、n>0となるようにk>0を取れればよいという考え方です。

[63] mixiユーザー 11月15日 18:32

みなさんお久しぶりです。
私の日記に書いた問題ですが、こちらにもアップしてみます。

【問題】

ある自然数Nが下の条件を満たすとします

条件：Nを素因数分解したとき、すべての素因数の指数は2以上となる

このような条件を、連続する２つの自然数が満たす組み合わせ(N,N+1)

を見つけてください

[64] mixiユーザー 11月15日 20:16

> パルキーさん

２乗の数がくさいな～とゆーことで探してますが…

まだ（８，９）しか見つかってません

[65] mixiユーザー 11月15日 20:18

（２８８，２８９）もかな？

[66] mixiユーザー 11月15日 21:23

なるほど。
二乗で考えてみると、
9800と9801なんかもありますね

それにしても難しい...

[67] mixiユーザー 11月15日 21:52

> paka&wandさん

一瞬、パソコンのＰＣ９８０１を思い出しましたｗ

[68] mixiユーザー 11月16日 03:04

N≦1億で
(8,9)
(288,289)
(675,676)
(9800,9801)
(12167,12168)
(235224,235225)
(332928,332929)
(465124,465125)
(1825200,1825201)
(11309768,11309769)
の10個でした。

[69] mixiユーザー 11月16日 03:08

上はプログラムを作って３時間以上かけて得たものですが、
↓こちらに答えがありましたorz
http://www.research.att.com/~njas/sequences/A060355

[70] mixiユーザー 11月16日 06:44

おお！答えがあるんですか！
出題した私もある本からの引用なんですが……

一応答えとしては無限個存在します。以下証明

【証明】

n,mが条件を満たすとき、積nmも条件を満たすということから、

(N,N+1)が条件を満たす⇒4Nも満たす⇒4N(N+1)も満たす

ここで4N(N+1)+1=(2N+1)^2であることから4N(N+1)+1も条件を満たす

よって

(N,N+1)が条件を満たす⇒(4N(N+1),4N(N+1)+1)も満たす

これは解の一部しか求まりません。

N=8を代入すると、4N(N+1)=288から(288,289)のペアが見つかりますが、
(675,676)や(9800,9801)は見つかりません。

[71] mixiユーザー 11月16日 07:44

整数列辞典の方にも同じ証明が書いてありますね。面白い証明だなあ。

他の解の生成公式を考えてみます。

[72] mixiユーザー 11月17日 23:57

wikipediaに多冪数という項がありました。
http://ja.wikipedia.org/wiki/%E5%A4%9A%E5%86%AA%E6%95%B0
結構研究されているみたいです。

それによると、x^2-8*y^2=1で表されるペル方程式が
整数解を無限に持つことから、解が無限に持つことが示されるそうで、
この場合は最小の自然数解が[x,y]=[3,1]であることから、
一般解は
a+b=6,ab=1,k=1,2,3...のときの
[x_k,y_k] = [(a^k+b^k)/2,(a^k-b^k)/(a-b)] (n,n+1)=[8*y^2,x^2]
と表され
実際に計算してみると、
[x_1,y_1] = [(a+b)/2,1] = [3,1] ∴(n,n+1)=(8,9)
[x_2,y_2] = [{(a+b)^2-2ab}/2,a+b] = [17,6] ∴(n,n+1)=(288,289)
[x_3,y_3] = [(a+b)(a^2-ab+b^2)/2,a^2+ab+b^2] = [99,35] ∴(n,n+1)=(9800,9801)
...
となって確かに題意を満たします。

[73] mixiユーザー 11月29日 01:09

新しいネタです。

累乗数キリ番をやっていたら、
134,689＝367^2
となりました。

十進法表記に限った話ですが、この平方数は、後の数字ほど大きくなっています。
この条件を満たす累乗数で、この直前の数と、この直後の数（もしあれば）を教えてください。

ちなみに、私はまだ調べていません。

[74] mixiユーザー 11月29日 08:10

カタラン予想(2002年に証明済み)によると、

x^a - y^b = 1　(x, y, a, b > 1の自然数)

となるx, y, a, bは

x=3, a=2, y=2, b=3

のみらしいです。

なので、累乗数の差が 1 となるのは、8 と 9 の組み合わせのみです。

[75] mixiユーザー 11月29日 12:31

＞binjiさん
全解です。
0=0^2
1=1^2
4=2^2
9=3^2
16=4^2
25=5^2
36=6^2
49=7^2
169=13^2
256=16^2
289=17^2
1369=37^2
13456=116^2
13689=117^2
134689=367^2

[76] mixiユーザー 11月30日 00:16

>75

らすかるさん、ありがとう。
これは、平方数についての全解ですね。
134689は、これだけでも顕彰すべきキリ番だとわかりました。

ところで、累乗数全体の中でも、最後でしょうかねえ。。

[77] mixiユーザー 11月30日 01:46

勝手に平方数と思ってしまっていました。
累乗数であれば以下が全解です。
（8,27,125,128が加わっただけです。）
0=0^n
1=1^n
4=2^2
8=2^3
9=3^2
16=2^4
25=5^2
27=3^3
36=6^2
49=7^2
125=5^3
128=2^7
169=13^2
256=2^8
289=17^2
1369=37^2
13456=116^2
13689=117^2
134689=367^2

[78] mixiユーザー 11月30日 23:40

↑ありがとうございます。

○立方数以上では、256
○立方数以上であって平方数でない数では、128
で打ち止めですね。

制約条件が、厳しく働きましたねえ。。

[79] mixiユーザー 12月01日 01:51

右辺にも2桁以上の数が6個（2^8=16^2とすれば7個）ありますが、
これらもすべて「非減少」ですね。

[80] mixiユーザー 12月01日 01:57

↑あ、本当ですね。
これは必然でしょうかねえ。。

[81] mixiユーザー 05月16日 17:45

このトピでは、たいへんお久しぶりです。
ご挨拶代わりに出題します。

a,b,c,dはすべて10以上50未満の自然数で、互いに異なっており、以下を満たします。
・ab=cd.
・a≡c (mod10)
・b≡d (mod10)
このようなa,b,c,dの組を、すべて求めてください。

[82] mixiユーザー 05月16日 23:57

最近、受付番号1377番をもらい、
1377=17*81=27*51.
に気づきました。
こういうふうに、1の位の組み合わせが同じである2数の積で表される場合を調べてみましたが、a,b,c,dがすべて2桁の自然数である場合は、かなり多くなりました。
値切って「50未満」という条件で問題にしてみました。

問題では簡単に「a,b,c,dの組」と書いてしまいましたが、これでは実質的に同じ組が4通りに表記されてしまいます。
答えていただける場合、最小である数をaとして、上の例ならば
(17,81,27,51)
というふうに書いてください。

それでは、もしこちらを巡回していただけたら、よろしくお願いします。
ジュニア問題ですから、思いつく限りで出していただければ結構です。

[84] mixiユーザー 05月24日 00:52

(10,45,30,15),(12,48,32,18),(13,46,23,26),(14,48,24,28)
という答を用意していました。
これで数え上げできていると思っていますが、いかがでしょうか。

どなたか、ここをご覧になっている方がいらっしゃるかなあ。

[85] mixiユーザー 05月24日 01:19

答えは
(10,45,30,15),(11,42,21,22),(12,44,22,24),(12,48,32,18),(13,46,23,26),(14,48,24,28)
の6個だと思います。

[86] mixiユーザー 05月24日 09:29

ご覧いただけて、安心しました。

私は何か勘違いして、はじめに11の倍数を排除していました。
らすかるさんの回答が正解でしょう。
単に数え上げただけですから、確証はないですけれども。

ログインすると、残り47件のコメントが見れるよ