[mixi]素朴な問いをお書きください - 曲線・曲面の多項式

[35] mixiユーザー 10月29日 00:42

こんばんは、不案内ですが
微分幾何の話についてゆけるようにしたいです。

すでに専門的に学ばれていると思いますので、
逆に、こういうことではないですか、というご確認の
お話です。

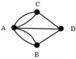
まず平面曲線Cの点pでの曲率は、点pで曲線Cに接する円の
半径rの逆数の値です。

これを足ががりにして、曲面Sの点pでの法線Nを含む平面族
を考えます。
これは法線が乗っている平面Πを
法線Nを軸として回転した平面の集まりをご想像ください。

それらが曲面Sと交わるとそれぞれ交線Cができます。
そのそれぞれの曲線Cに、点pで接する円の半径の逆数を
考えます。
これは曲線Cの点pでの曲率です。

それらの曲率の中での最大値と最小値の積が、
ガウス曲率だそうです。

参考文献
[1]長野正『曲面の数学』培風館

ガウス曲率の定義の部分に少し幾何学的な意味が
書いてありましたので機会がありましたらご参照ください。

それではまた。

[36] mixiユーザー 10月29日 01:07

「接する円」の訂正ですが、

接するというだけでは無数に存在しますので、

「接する円」というよりも、もっと
条件が強くて、パラメータ表示の関数の二階導関数まで
一致ということでした。
いわゆる2位の接触というものです。

すみません。

[38] mixiユーザー 02月20日 11:56

Thom の基本カタストロフィ曲面、６つまでわかったのですが、もうひとつはどのような式でしょうか？

[39] mixiユーザー 02月20日 11:58

追加

[41] mixiユーザー 01月14日 20:52

以下がアンデュロイドの場合のFunction Viewの設定内容です。
お試しください。

■媒介変数 f(t)の入力

∫[0,t](sqrt(1+2*a*cos(x)+a*a)/(1+a*cos(x))^2)dx+1/(1+a*cos(t))*(-a*sin(t))/sqrt(1+2*a*cos(t)+a*a)

■媒介変数 g(t)の入力

cos(s)*(1/(1+a*cos(t))*(1+a*cos(t))/sqrt(1+2*a*cos(t)+a*a))

■媒介変数 h(t)の入力

sin(s)*(1/(1+a*cos(t))*(1+a*cos(t))/sqrt(1+2*a*cos(t)+a*a))

■tの範囲
-2*π ～ 2*π

■aの値

0.5など

■マクロ

onload 描画

on a change 描画

sub 描画()#1
s=0
cls
afimageon
for s=0 to 2pi step pi/20
draw
next s
afimageoff
end sub

-----------------------------------------------------------

取り急ぎ、アンデュロイドの式については以下のWebページを参考にしました。
http://www.geocities.jp/ikuro_kotaro/koramu/korogaru.htm

・アンデュロイドの補足

楕円Eが直線Lの周りをすべることなく転がると、楕円の焦点Fが曲線Γを描き、
その曲線Γを直線Lの周りに回転した回転面がアンデュロイド
だそうです。
そのため、パラメータ表示に楕円の弧の長さの計算が必要です。

楕円が円や楕円の周りをすべることなく転がるとき、
閉じた曲線が出来れば、それは代数曲線の一部分かどうか、
これなどは素朴な疑問です。

[43] mixiユーザー 01月20日 14:12

・41番の文について
cos(s)*(1/(1+a*cos(t))*(1+a*cos(t))/sqrt(1+2*a*cos(t)+a*a))
sin(s)*(1/(1+a*cos(t))*(1+a*cos(t))/sqrt(1+2*a*cos(t)+a*a))
→
cos(s)/sqrt(1+2*a*cos(t)+a*a)
sin(s)/sqrt(1+2*a*cos(t)+a*a)

急いで書いたため約分し忘れていました。

aの値を1より大きくするとノドイドが出てくると思ったのですが、
形が多少違う様子です。

どういう形になるかというのが以下のWebページでJava Appletにより
見れます。(unduloidとnodoid以外の平均曲率一定曲面(CMC surface)
もあります。)

York大学 Gallery of Surfaces
http://www-users.york.ac.uk/~im7/surfaces.html

/////////////////////////////////////////////////////////////////////

[44] mixiユーザー 07月29日 04:14

包絡線についてなんですが
αを助変数とする方程式
f(x1,x2,α) =0
のすべての曲線に接する曲線Ｃですが
Ｃと曲線f(x1,x2,α) =0が接する点において
f(x1(α),x2(α),α) =0
が成立するから　その両辺をαについて微分すれば
∂f/∂x1 dx1/dα +∂f/∂x2 dx2/dα +∂f/∂α =0
またＣの接線ベクトル（dx1/dα,dx2/dα ）はf(x1,x2,α) =0
に接するから
∂f/∂x1 dx1/dα +∂f/∂x2 dx2/dα =0 ....?
という?がなんで言えるのかわかりません
何故でしょうか？

[45] mixiユーザー 07月29日 22:15

もし間違っていましたらすいませんが、意味的には
∂f/∂x1 dx1/dα +∂f/∂x2 dx2/dα
は法線ベクトル(∂f/∂x1,∂f/∂x2)と接線ベクトル(dx1/dα,dx2/dα)
の内積で、それらのなす角が±π/2なのでではないでしょうか。

補足ですが、それにより f(x1,x2,α)=∂f(x1,x2,α)/∂α=0 という式が
包絡線の定義式になるはずです。曲面の族 f(x1,x2,x3,α)=0 の場合も
同様だったと思います。

[46] mixiユーザー 08月03日 09:05

WEBで見かけたんですが、
f(x1,x2,α) =0　を空間曲線と見て
それをx,y平面に押しつぶすイメージで
α方向の微分係数がゼロ　すなわち
∂f(x1,x2,α)/∂α=0
が必要ということでした
なるほど納得です

[47] mixiユーザー 10月08日 01:50

はじめまして

３次ベジエ曲線の勉強をしています。

質問なんですが

１本の３次ベジエ曲線を、任意のパラメータt1～t2で切り取り、切り取った部分の３次ベジエ曲線の制御点を求める方法がありましたら教えていただけないでしょうか。

[48] mixiユーザー 10月09日 00:23

こんにちは。ちょっと考えてみました。(ただし、完成はしていないのですが)

問題の設定を単純なケースにして、

制御点(x_0,y_0),(x_1,y_1),(x_2,y_2),(x_3,y_3) に対するベジエ曲線C
のパラメータをtとして、tの動く区間は[0,1]とし、これを3等分した
特殊なケースだけ計算します。

tを区間[1/3,2/3]に部分的に制限してできる、Cの部分曲線C'について、
それに対する制御点(g_0,h_0),(g_1,h_1),(g_2,h_2),(g_3,h_3) を得ること

がこの場合の問題です。

ここで、τ:=3(t-1/3) として変換して、τが[0,1]を動くようにして、
x成分だけ書くとすれば、その式は

x=(1-t)^3*x0+3*t*(1-t)^2*x1+3*t^2*(1-t)*x2+t^3*x3
x=(1-τ)^3*g0+3*τ*(1-τ)^2*g1+3*τ^2*(1-τ)*g2+τ^3*g3

なので、τを消去してから両方の差を取って、それが恒等的に0なので
tの4つの次数の係数が0となって、連立代数方程式が出ます。

ここから、g0,g1,g2,g3をx0,x1,x2,x3で表すような変形をするのですが、
計算機代数ソフトで端折ります。以下はRISA/ASIRのコードです。

↓C:\bezier.txtのソースコード
def test()
{
T=(t+1)/3;
XA=(1-T)^3*x0+3*T*(1-T)^2*x1+3*T^2*(1-T)*x2+T^3*x3;
XB=(1-t)^3*g0+3*t*(1-t)^2*g1+3*t^2*(1-t)*g2+t^3*g3;
DX=XA-XB;
L=[coef(DX,3,t),coef(DX,2,t),coef(DX,1,t),coef(DX,0,t)];
G=gr(L,[g0,g1,g2,g3],2);
}
end$

↓RISA/ASIRのコマンド
load("c:\\bezier.txt");
load("gr);
G=test();
[x0+6*x1+12*x2+8*x3-27*g3,2*x0+9*x1+12*x2+4*x3-27*g2,-4*x0-12*x1-
9*x2-2*x3+27*g1,8*x0+12*x1+6*x2+x3-27*g0]

↓結果から手計算
g0=(8*x0+12*x1+6*x2+x3)/27
g1=(-4*x0-12*x1-9*x2-2*x3)/(-27)
g2=(2*x0+9*x1+12*x2+4*x3)/27
g3=(x0+6*x1+12*x2+8*x3)/27

・y方向も全く同様です。

代数的にしか確かめてませんので、もし図が書けたら追加します。

[50] mixiユーザー 10月13日 17:12

48番の文は少し分かりづらい説明でしたが、連立一次方程式なので線型代数の範囲でも解けます。
区間[0,1]上のパラメータ表示から一意的に4点が決まるのがポイントです。

より一般にtの区間[0,1]を区間[a,b]に制限して解いてみます。
tの区間[a,b]をτの区間[0,1]に移す変換がτ=(t-a)/(b-a) , すなわち t=(b-a)τ+a です。
そこで、上のソースコードで T=(t+1)/3; を T=(b-a)*t+a; に変えて同様に計算すると、
c:=1-a,d:=1-bと置いたときに(RISA/ASIRと手計算により)

g0 = x0*c^3 + 3*x1*a*c^2 + 3*x2*a^2*c + x3*a^3
g1 = x0*(c^2*d)
+ x1*(-3*c*d + c + 2*d)*c
+ x2*(-3*a*b + a + 2*b)*a
+ x3*(b*a^2)
g2 = x0*(c*d^2)
+ x1*(-3*c*d + 2*c + d)*d
+ x2*(-3*a*b + 2*a + b)*b
+ x3*(b^2*a)
g3 = x0*d^3 + 3*x1*b*d^2 + 3*x2*b^2*d + x3*b^3

となり、x0,x1,x2,x3をy0,y1,y2,y3にかえてg0,g1,g2,g3をh0,h1,h2,h3
に改めると制御点は(g0,h0),(g1,h1),(g2,h2),(g3,h3)
となります。

図を2つほど載せておきます。

・用途は分かりませんが、切り取った部分の制御点を少し変えるとしたら、
滑らかさが失われるので、別の工夫がいりそうな気がします。しかし
一部取り除くには上式は便利かもしれません。(区間[0,a]と[b,1]だけ
残してそれぞれの制御点を上式から記号を改めて出すといったふうです)

[51] mixiユーザー 10月13日 18:21

>非線型都市さん

ありがとうございますo(^-^)o参考になりました!!

最終的にはド・カステリョのアルゴリズムを２回使う方法で実装しました。

[52] mixiユーザー 10月13日 22:48

> ド・カステリョのアルゴリズム

こちらこそ勉強になりました。
おそらく図のような感じで内分点を出すのでしょう。

[53] mixiユーザー 10月13日 23:10

>非線型都市さん

そんな感じです!!

また聞きたいことがあれば書き込みます。

[55] mixiユーザー 11月19日 22:12

どうもはじめまして。
私はこの定理や分野をよく知らないため、
一応管理人の役目かどうかは別としまして、どなたかにフォローをお願いしたいと思います。

(ご確認ですが)下のページの論文の内容が、その定理の出展でしょうか?

[1] Bernštein, S.
"Sur un théorème de géométrie et son application aux équations aux dérivées partielles du type elliptique. "
Charĭkov, Comm. Soc. Math.

http://www.zentralblatt-math.org/zmath/en/search/?q=an:48.1401.01&format=complete

また、[1]を参照している次の論文の最初のページは見ることができました。
(少しだけですが)

[2] Manfredo P. do Carmo and H. Blaine Lawson, Jr. "On Alexandrov-Bernstein theorems in hyperbolic space"
Duke Math. J. Volume 50, Number 4 (1983), 995-1003.

http://projecteuclid.org/DPubS?verb=Display&version=1.0&service=UI&handle=euclid.dmj/1077303486&page=record

・素人ながらGoogle Scholarで調べてみただけです。お役に立てなくてすみません。
もっと有益な情報(関連する興味深い結果・本や論文の題など)がいただければと思います。

思わぬつながりなどがあると面白いので、
ご紹介いただければ参考になります。
具体的な自明でない例や図があると助かります。

コミニュテイの趣旨としては今後は
文献がどういうものがあるかという情報の交流もいろいろ
あるとよいでしょう。

それと微分幾何やリーマン幾何に関する話題は今後もありえるので
トピックを立てていただいてそこで議論されていただくとよいと思います。

[57] mixiユーザー 11月22日 18:24

どうもはじめまして

私は大学院で曲面について勉強しているのですが，だいたい完備な曲面について考えているんです。ところで曲面論での『完備』っていったいどのような意味をなしているのでしょうか？？

簡単にいうと曲面上の測地線が無限につづくことを完備というのです（穴があると困るみたいなこと）。この完備性が仮定にある定理がいくつもあるし，自分でなにか考える上でも完備な曲面として考えます。

あたりまえのような…
完備でない曲面の例とかありますか？

最近では完備性はただの飾りみたいに思ってしまいます。疑問があまり明確でないのですが，私の疑問が晴れるようなことがあればどなたかお願いします。

「bernsteinの定理」についてはであったことないので分かりませんが，結論はおもしろいですね～！「mathematicaの曲線と曲面の微分幾何」等で極小曲面と複素数とのからみを理解してればできそうって気持ちです！！

では～

[58] mixiユーザー 11月24日 06:06

はじめまして。

完備でない曲面の例ということですが、完備な距離空間から点を除くと出来そうな気がします。

話を進めやすいようにより厳密に書いてみます。

リーマン多様体をMとしたとき
Mが完備
⇔
(1) Mは完備距離空間
(2) Mの任意の点pの接空間T_p(M)が、部分集合T~_p(M)と一致
　　(ここで、T~_p(M) := {v ∈ T_p(M) | ある測地線γ:[0,1]→M で γ(0)=p, γ'(0)=v となるものが存在})
(3) Mの任意の閉距離球はコンパクト
(閉距離球はMの点p,正数εについての{q ∈ M | d(p,q)<=ε}のこと)

(ただし岩波数学辞典第4版の「257 大域リーマン幾何学」の項などを参考にしました)

そうすると、
条件(1)はMが一般の距離空間というだけならば、
完備な距離空間X~の、稠密な真部分集合M (例. 実数の直積に対する有理数の直積) でよさそうですが、
MがC^∞級多様体となると、もっと普通の多様体らしい例があるほうがよいです。

条件(3)を満たさない例は、1次元のユークリッド距離空間の開区間(0,1)をMとすると
半径1/2以上のときなどコンパクトでないといった例が取れそうです。

条件(2)を満たさないケースは想像が付きません。
Mを扇形のようにしてみただけではうまくゆかなさそうに思います。

もし論理的な欠陥がありましたら教えてください。

[59] mixiユーザー 11月24日 07:06

ありがとうございます！！きっと阿呆な質問に答えていただいてありがとうございます！

(2)についてはちょっとよくわかりません。(3)を認めてあげると，なんかおもしろい曲面ができそうなんだが…

私も岩波数学辞典第3版(あれはむずい！)を読んでみました。
なんか(1)⇔(2)⇔(3)のように書いてありました。うんわからない。

いちよう岩波講座基礎数学「微分幾何学?」(佐々木重夫)にそれらしいことがかいてありますが，大域的と局所的，接続可能と接続不可能とか…完備とは，微分幾何学の大域的考察にもっとも適しているそうなのですが，「きたない多様体もあつかおうぜ！！」ってなればよいのに…

なにかあればよろしくお願いします。

[60] mixiユーザー 11月29日 16:47

(1)から(3)が同値というのは見落としていました。すみません。
しかし58番の文の例を少し考えると(1)⇔(3)がほとんどだろうという印象でした。

それに関してもう一つ例ですが、
R^2(2次元ユークリッド距離空間)から点(1/2,0)を除いたMの場合も、完備で無い開集合です。

しかもその中にある、中心(0,0),半径1の閉距離球{(x,y)∈A | x^2+y^2<1}は
コンパクトにならないです。

さらに除く点が有限個増えても同様ですし、さらに空で無い閉集合を除いた
多様体もだいたい同様というふうに考えられます。

そうすると直感的な説明と結びついて、
「穴がある」とか
「地面を測地線に沿って進むとどこかの方向ではいきどまりになる」
「円盤が空間の中を飛び回ると空間からはみ出る」
ようなことがあるのは完備でないと思っておけば、関連する定理の仮定が少し覚えやすいのかもしれません。

・同じ開円板でも普通の距離と、双曲幾何のポアンカレ・モデルの場合では、
後者は端に近づくと距離が1でも絵の見た目では短くなってゆくので、
いつまでも進んでいられる意味で完備かもしれません(違っていたらすみません)

・「大域と完備」というキーワードでいうと代数多様体もそういうような似た概念があります。
　その場合、たとえば
　アフィン平面 : 完備でない
　射影平面 : 完備
　です。確かに代数曲線は射影平面まで考えると大域的な性質が
　いろいろと出てくるようです。
　完備な多様体が大域的な性質を調べるのに適したものといわれると、そんな気がします。

[61] mixiユーザー 11月29日 16:50

訂正です。
> 中心(0,0),半径1の閉距離球{(x,y)∈A | x^2+y^2<1}
訂正後
> 中心(0,0),半径1/2の閉距離球{(x,y)∈A | x^2+y^2<=1/2}

[62] mixiユーザー 11月29日 18:02

へー！へーー！！なるほど～！ありがとうございます。

アフィン変換は完備ではないのですか！
「円盤が空間の中を飛び回ると空間からはみ出る」ってのもおもしろいですね～
大域的に考えるには，やっぱり定義できないであろう点の扱い方がポイントなんですね！ありがとうございました。

> 中心(0,0),半径1/2の閉距離球{(x,y)∈A | x^2+y^2<=1/2}
訂正
> 中心(0,0),半径1/2の閉距離球{(x,y)∈A | x^2+y^2<=(1/2)^2}

[63] mixiユーザー 11月29日 19:26

半径2乗し忘れました。ご指摘ありがとうございます。

ところでアフィン変換というよりこの場合ですとアフィン空間です。
アフィン空間の一種である複素平面3つを貼りあわせて、
ある複素多様体(射影平面)を得るのですが、そこまで拡張してでないと、
都合が悪いことが多いわけです。

難しいことは省きますが、完備の定義がだいぶ違うので、
ユークリッド空間に普通の距離を入れると完備距離空間だけれども
代数多様体の意味では完備でないということもあります。
そこに距離やコーシー列といった概念は出てきません。

[64] mixiユーザー 11月29日 19:45

重ねてすいません。
双曲幾何のポアンカレ・モデルと書きましたが単位円板モデルに訂正します。

[65] mixiユーザー 10月25日 05:25

Ｍａｔｈｅｍａｔｉｃａで以下の図形を表示するコマンドを教えてください
x^3+y^3 =1 x,y ∈C

補足
複素数関数のフェルマー的球面の表示です
なんかの数学啓蒙書にこの図が載ってたのですが
どうプロットすればいいか分らないんです

[66] mixiユーザー 10月29日 23:27

ご無沙汰しております。書籍が分りましたら教えていただければと思います。

Mathematica のコマンドの方法はわかりませんが、
こちらで次のようなパラメータ表示を考えてみました。

有理変換で y^2={3次式} に持ち込んだりと、ほかにもあるにはあるのですが
図が描きにくそうなので、
安易に初等関数の計算方法であらわしてみました。

まず y=tx としておいて x^3+(tx)^3 = 1 を x について解くと
　x = (1+t^3)^(1/3)
でして、 t を複素数にまで拡張して t = r e^{iθ} と置きます。そのとき
　x = {(1 + r cosθ)^2+r^2 sin^2 θ}^{-1/6} *
　 [ cos{1/3 atan(r sinθ/(1+rcosθ)) } + i sin {1/3 atan(r sinθ/(1+rcosθ)) }]
　y = r * (cosθ+isinθ) * x
となり、
さらに変形していって、
　x = x_1 + i x_2
　y = y_1 + i y_2
と書いて点(x_1,x_2,y_1,y_2) が r,θであらわされます。

そうしておいて、

(1) そのなかから3つの (x_1,y_1,y_2) を選びプロットします。
　　残念ながらMahtematicaをもちあわせていなかったため
　　3D-XplorMath-J で描かせてみました。塗りつぶす前にワイヤーフレームだけが出てきたのでその図も付しておきます。
　　曲線の族が描かれ、Fermat曲線の部分と似た形が見て取れます。
　　Mahtematicaの図ではもっときれいかもしれません。
　　
　　入力した式は以下です。(変数x,yは上のと異なる意味です)
x = ((1+u*cos(v))^2+u^2*(sin(v))^2)^(-1/6) * ( cos(1/3*atan((u*sin(v)/(1+u*cos(v)) ))) )
y = ((1+u*cos(v))^2+u^2*(sin(v))^2)^(-1/6) * u*( ( cos(1/3*atan((u*sin(v)/(1+u*cos(v)) ))) ) * cos(v) - (-sin(1/3*atan((u*sin(v)/(1+u*cos(v)))))) * sin(v) )
z = ((1+u*cos(v))^2+u^2*(sin(v))^2)^(-1/6) * u*( ( cos(1/3*atan((u*sin(v)/(1+u*cos(v)) ))) ) * sin(v) + (-sin(1/3*atan((u*sin(v)/(1+u*cos(v)))))) * cos(v) )

　　(範囲は 0<= u <=10 , -6.28 <= v <=6.28 , u,vの解像度 40です。)

(2) それだけで物足りない場合は、
点(x_1,x_2,y_1,y_2)を回転して、
　　点(X_1,X_2,Y_1,Y_2)に移したときの点(X_1,Y_1,Y_2)などの図や動画なども作ってみるといかがでしょう。
　　それには各軸の回転行列を合成して変換すればよいので、 Mathematicaのようにプログラムがある程度作成できれば
　　楽にできることでしょう。
　　
　　そういう動画を見るうちに、もしかしたら同相写像でトーラスになることがちょっとは想像できるのかもしれないですね。

[67] mixiユーザー 10月30日 19:35

訂正
x = (1+t^3)^(1/3)
でなく
x = (1+t^3)^(-1/3)
です。すみません。

あと最後の行の補足としては同相写像でトーラスになるには無限遠点も
必要でしょう。
また4次元図形の描画の方法ですが、上記のような単純な射影よりも
もっと視覚的に把握しやすいように工夫が必要と思います。

[68] mixiユーザー 10月31日 12:39

さらに訂正です。すみません。

訂正前
　x = {(1 + r cosθ)^2+r^2 sin^2 θ}^{-1/6} *
　 [ cos{1/3 atan(r sinθ/(1+rcosθ)) } + i sin {1/3 atan(r sinθ/(1+rcosθ)) }]
訂正後
　x = {(1 + r^3 cos3θ)^2+r^6 sin^2 (3θ)}^{-1/6} *
　 [ cos{1/3 atan(r^3 sin(3θ)/(1+r^3 cos(3θ))) } + i sin {1/3 atan(r^3 sin(3θ)/(1+r^3 cos(3θ))) }]

入力する式が以下のように変わります。
x = ((1+u^3*cos(3*v))^2+u^6*(sin(3*v))^2)^(-1/6) * ( cos(1/3*atan((u^3*sin(3*v)/(1+u^3*cos(3*v)) ))) )
y = ((1+u^3*cos(3*v))^2+u^6*(sin(3*v))^2)^(-1/6) * u*( ( cos(1/3*atan((u^3*sin(3*v)/(1+u^3*cos(3*v)) ))) ) * cos(v) - (-sin(1/3*atan((u^3*sin(3*v)/(1+u^3*cos(3*v)))))) * sin(v) )
z = ((1+u^3*cos(3*v))^2+u^6*(sin(3*v))^2)^(-1/6) * u*( ( cos(1/3*atan((u^3*sin(3*v)/(1+u^3*cos(3*v)) ))) ) * sin(v) + (-sin(1/3*atan((u^3*sin(3*v)/(1+u^3*cos(3*v)))))) * cos(v) )

図を描くとだいぶ形が変わりました。

[69] mixiユーザー 11月01日 23:31

>非線型都市さん
大変な労作　返答ありがとうございます
ただこの式　複雑すぎてMathematicaに翻訳して
打ち込むのがタイヘンです
ボチボチやってみます

[70] mixiユーザー 03月25日 08:20

例のフェルマー的曲面　参考文献があって
簡単な式が載ってたのですが
うまくプロット出来ません
画像の一番上の式です

次の行からはクレプシュの３次曲面をプロットしたいのですが
これもうまく行きません
Mathematica 4.1です

どなたか、プロット出来る方法
ご教授願います

[71] mixiユーザー 12月23日 13:27

Calc-Plusというフリーウェアでクレプシュ曲面描画できました
これを使って前のフェルマー的球面のパラメータ表示
ご教示頂いたのでやってみようと思います

[72] mixiユーザー 12月27日 20:50

フェルマー曲面　Mathematicaで定義してみたのですが
以下のメッセージが取れません

[73] mixiユーザー 12月27日 23:19

ご無沙汰しております。
もう少し簡単な式になりますので、
そちらをお使いいただけますでしょうか。
疑似コードにて紹介させていただきます。

################################
Input: u,v
Output: x1,x2,y1,y2

r := 1/( (1+(u^3)*cos(3*v))^2 + u^6*(sin(3*v))^2 )^(1/6);

s := -1/3 * atan2( u^3 * sin(3*v) , 1 + u^3 * cos(3*v) );

x1:= r * cos(s);
x2:= r * sin(s);
y1:= u * r * cos(s+v);
y2:= u * r * sin(s+v);
################################

(但しu<2, atan2(y,x)=atan(y/x) (x>0, y>0), 原点中心, 反時計回りの, ベクトル(1,0)からベクトル(x,y)への角[rad] , MathematicaのArcTan(2変数))

ログインすると、残り40件のコメントが見れるよ