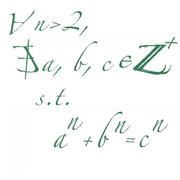数学コミュのウィトゲンシュタインの数学観から

「論理哲学論考」の中に注目すべき言葉がある

　　６．０２１　数は操作の冪（べき）である。
　　６．０３　　整数の一般形式はこうである。　[ ０，ζ，ζ＋１　]
　　６．０３１　集合論は数学ではまったくよけいである。
　　　　　　　　このことは数学において要求される一般性が偶然的なもの
　　　　　　　　ではないことと結びついている。

　ウィトゲンシュタインの数学観を認める数学者はほとんどいない。あまりに素朴すぎて、これでは数学と言うより算術にしかならない。一番の問題は、数が単に繰り返しの操作でしかなければ無限集合というものを考えることが出来ないことになる。無限集合という考え方がなければ現代数学の成果というものはかなり貧弱なものとなってしまうだろう。

　数学者がウィトゲンシュタインの数学観を幼稚だと切り捨てるのも理解できるが、彼をそんなに軽んじても良いものだろうかという気もする。無限集合は言葉では矛盾なく定義はできる。しかし、我々の能力では(少なくとも私の能力では)それを直観することは出来ない。例えば対角線論法による証明は何度説明を受けてもはぐらかされた気分になる。

　無限とは文字通り「限りがない」ということで、我々には到達できないという意味ではなかっただろうか。「無限」をさも自家薬籠中のもののごとく扱っている現代数学には一種の妖しさがつきまとっているような気がしてならない。

　この件について皆さんのご意見を伺いたいと思います。

コメント(1)

最初
全て
最新の40件

[1] mixiユーザー 09月11日 09:32

　現代数学では矛盾なく定義できるものはすべて数学的実体として取り扱うことが出来るが、それがなにを意味するかを直観出来ないものがある。

　例えば、ℕを「すべての自然数からなる集合」と定義してみれば、ℕに矛盾はない。例えば√２や1384657というようなどんな数字でも（あるいはリスや机でもなんでもよい）、それに含まれるかどうかは明晰である。しかし、ℕそのものを思い浮かべることは不可能である。
また、連続とい概念は「ε-δ論法」によって矛盾なく定義できる。しかし、数直線上の１点に直接隣り合う一点は存在するのかしないのかが直観できない。

　直観できないものを自明のごとく取り扱うことにある種の戸惑いを感じる。数学者から見れば素朴すぎるということになるのかも知れないが‥‥。

ログインすると、みんなのコメントがもっと見れるよ