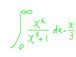2010年12月19日 23:52
http://
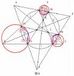
の (88)の ●もかい●が 明記してある f[x]について、
(1)Exampleに倣い 下の 各々について 有理係数の 多項式 表現を;
f2[x]=(x - α^2)*(x - β^2)*(x - γ^2)=
f3[x]=(x - α^3)*(x - β^3)*(x - γ^3)=
.
f7[x]=(x - α^7)*(x - β^7)*(x - γ^7)=
(2)各fj[x]について(88)のような●もかい∈Q[α]●を求め、Gal(E/Q)を求めてください;
f2[ ]=0 , Gal(E/Q)=
f3[ ]=0 , Gal(E/Q)=
.
f7[ ]=0 , Gal(E/Q)=
(3)皆んな 「盥回し 即 C3 」に なりましたか?(なったなら 其の所以は?)
>終結式、不変式など 2008年08月12日 11(★只今 2010 12 19★)
>定 理 対称式は、基本対称式の多項式として表せ、その表し方は一意的である。
http://
http://
の (88)の ●もかい●が 明記してある f[x]について、
(1)Exampleに倣い 下の 各々について 有理係数の 多項式 表現を;
f2[x]=(x - α^2)*(x - β^2)*(x - γ^2)=
f3[x]=(x - α^3)*(x - β^3)*(x - γ^3)=
.
f7[x]=(x - α^7)*(x - β^7)*(x - γ^7)=
(2)各fj[x]について(88)のような●もかい∈Q[α]●を求め、Gal(E/Q)を求めてください;
f2[ ]=0 , Gal(E/Q)=
f3[ ]=0 , Gal(E/Q)=
.
f7[ ]=0 , Gal(E/Q)=
(3)皆んな 「盥回し 即 C3 」に なりましたか?(なったなら 其の所以は?)
>終結式、不変式など 2008年08月12日 11(★只今 2010 12 19★)
>定 理 対称式は、基本対称式の多項式として表せ、その表し方は一意的である。
http://
|
|
|
|
コメント(7)
(P_3)^2={(s_1)^3-3*s_1*s_2+3*s_3}^2
(α^3+β^3+γ^3)^2=α^6+β^6+γ^6+2*α^3β^3+2*α^3γ^3+2*β^3γ^3
公式より、
P_5=s_1*P_4-s_2*P_3+s_3*P_4-s_4*P_1+5*s_5
P_6=s_1*P_5-s_2*P_4+s_3*P_3-s_4*P_2+s_5*P_1-6*s_6
代入して、
P_5=(s_1)^5-5(s_1)^3s_2+5(s_1)^2s_3+5s_1(s_2)^2-5s_2s_3
P_6=(s_1)^6-6(s_1)^4s_2+6(s_1)^3s_3+9(s_1)^2(s_2)^2-12s_1s_2s_3-2(s_2)^3+3(s_3)^2
s_1=0, s_2=-1, s_3=1 なので、
P_1=0, P_2=2, P_3=3, P_4=2, P_5=5, P_6=5
(α^3+β^3+γ^3)^2=α^6+β^6+γ^6+2*α^3β^3+2*α^3γ^3+2*β^3γ^3
は、
(P_3)^2=P_6+2*(α^3β^3+α^3γ^3+β^3γ^3)
9=5+2*(α^3β^3+α^3γ^3+β^3γ^3)
(α^3β^3+α^3γ^3+β^3γ^3)=2
α^3β^3γ^3=(αβγ)^3=(s_3)^3=1
ここで、出そろいました。
(x-α^3)(x-β^3)(x-γ^3)=x^3-3x^2+2x-1
(α^3+β^3+γ^3)^2=α^6+β^6+γ^6+2*α^3β^3+2*α^3γ^3+2*β^3γ^3
公式より、
P_5=s_1*P_4-s_2*P_3+s_3*P_4-s_4*P_1+5*s_5
P_6=s_1*P_5-s_2*P_4+s_3*P_3-s_4*P_2+s_5*P_1-6*s_6
代入して、
P_5=(s_1)^5-5(s_1)^3s_2+5(s_1)^2s_3+5s_1(s_2)^2-5s_2s_3
P_6=(s_1)^6-6(s_1)^4s_2+6(s_1)^3s_3+9(s_1)^2(s_2)^2-12s_1s_2s_3-2(s_2)^3+3(s_3)^2
s_1=0, s_2=-1, s_3=1 なので、
P_1=0, P_2=2, P_3=3, P_4=2, P_5=5, P_6=5
(α^3+β^3+γ^3)^2=α^6+β^6+γ^6+2*α^3β^3+2*α^3γ^3+2*β^3γ^3
は、
(P_3)^2=P_6+2*(α^3β^3+α^3γ^3+β^3γ^3)
9=5+2*(α^3β^3+α^3γ^3+β^3γ^3)
(α^3β^3+α^3γ^3+β^3γ^3)=2
α^3β^3γ^3=(αβγ)^3=(s_3)^3=1
ここで、出そろいました。
(x-α^3)(x-β^3)(x-γ^3)=x^3-3x^2+2x-1
高木貞治さんの代数学講義、P169に例があった。
方程式f(x)=a_0*x^n+a_1*x^(n-1)+...+a_n=0の根
x_1,x_2,...x_3 の平方を根とする方程式を求めること。
求める方程式を、F(x)=y^n+A_1*y^(n-1)+...+A_n=0とすれば
A_1=-Σ(x_1)^2, A_2=Σ(x_1)^2(x_2)^2, A_3=Σ(x_1)^2(x_2)^2(x_3)^2,...
である。
ただしこの場合には、
(a_0)^2*F(y^2)
=(a_0)^2*II*(y^2-x_k^2)
=(a_0)*II*(y-x_k)*(a_0)*II*(y+x_k)
=f(y)*(-1)^n*f(-y)
だから、f(y)*f(-y)を計算してy^2にyを代入すれば、
(-1)^n*a_0^2*F(y)が得られる。
ゆえにF(y)の符号にかまわないならば、
a_0^2*A_1=-a_1^2+2*a_0*a_2,
a_0^2*A_2=a_2^2-2*a_1*a_3+2*a_0*a_4,
a_0^2*A_3=-a_3^2+2*a_2*a_4-2*a_1*a_5+2*a_0*a_6,
・・・・・・・・
a_0^2*A_n=(-1)^n*a_n^2
方程式f(x)=a_0*x^n+a_1*x^(n-1)+...+a_n=0の根
x_1,x_2,...x_3 の平方を根とする方程式を求めること。
求める方程式を、F(x)=y^n+A_1*y^(n-1)+...+A_n=0とすれば
A_1=-Σ(x_1)^2, A_2=Σ(x_1)^2(x_2)^2, A_3=Σ(x_1)^2(x_2)^2(x_3)^2,...
である。
ただしこの場合には、
(a_0)^2*F(y^2)
=(a_0)^2*II*(y^2-x_k^2)
=(a_0)*II*(y-x_k)*(a_0)*II*(y+x_k)
=f(y)*(-1)^n*f(-y)
だから、f(y)*f(-y)を計算してy^2にyを代入すれば、
(-1)^n*a_0^2*F(y)が得られる。
ゆえにF(y)の符号にかまわないならば、
a_0^2*A_1=-a_1^2+2*a_0*a_2,
a_0^2*A_2=a_2^2-2*a_1*a_3+2*a_0*a_4,
a_0^2*A_3=-a_3^2+2*a_2*a_4-2*a_1*a_5+2*a_0*a_6,
・・・・・・・・
a_0^2*A_n=(-1)^n*a_n^2
- mixiユーザー
- ログインしてコメントしよう!
|
|
|
|
独学ノート(土筆の子) 更新情報
-
最新のイベント
-
まだ何もありません
-
-
最新のアンケート
-
まだ何もありません
-
独学ノート(土筆の子)のメンバーはこんなコミュニティにも参加しています
人気コミュニティランキング
- 1位
- マイミク募集はここで。
- 89880人
- 2位
- 食べ物写真をつい撮ってしまう人
- 19406人
- 3位
- 暮らしを楽しむ
- 75792人