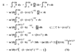一般相対性理論コミュのリーマン幾何学

もしご存じない方がおられたら、接続係数の参考になりそうかな

座標変換

岡部 洋一 放送大学教授 (東京大学名誉教授)
http://moge.org/okabe/temp/Riemann.pdf

（WEPを含む）等価原理を認めたら
「クリストッフエル記号のすべての成分が0であれば局所慣性係になるし、逆もまた真」となることが示せるかと思います


＞メビウスの輪みたいな宇宙だったら計量はどうなるんでしょうね。

さあ、どうでしょう
ただ、大局的にねじれたようなトポロジーでも、球面と同様の形式で表せるかなとは思います

メビウスの帯ってのはなんともおもしろい形だなあ
http://www.osaka-ue.ac.jp/zemi/nishiyama/math2010j/moebius_j.pdf
メビウス（A.F. Möbius，1790〜1868）は 19 世紀に活躍したドイツの数学者であり天文学者である．メビウスの帯は，彼が提唱したものでその名がついている．彼は天文学者でもあるので，宇宙の構造に興味があり，宇宙の果てはどうなっているのかといろいろ思いをめぐらしているうちに考案したものとされている

３次元ユークリッド空間内の平坦なメビウス帯の特異点
http://www.kurims.kyoto-u.ac.jp/~kenkyubu/bessatsu/open/B38/pdf/B38-09.pdf


以下の落書きは深く追及されても返答できませんが
書きたかったのでｗ

わたしは、現実に４次元は存在しないという世界観がありますので
たとえばねじれた帯を

｛　（３＋１）　＋　1　｝　次元

　　　　　↑　　　　↑
　　　　虚数　　光時間

のような拡大空間から
四元時空に投影して縮退させたものだと考えることで、
代数的に扱いやすくしたいのと、他のトポロジーの図形との関係性において一般化できないだろうかと思います
素数を複素数で因数分解するようなことを幾何でやる
こういうのを、かなり広い意味でホログラフィック原理と勝手に呼んでます
超平面みたいなことを考えていると言ってもいいのかな

あるいは、メビウス帯にしては必要以上に複雑になり過ぎるかもしれないが、対称性の高い複素多様体から四元時空に縮退させるとか

ブラックホールは局所的に時空各点でねじれ（符号反転）が起こっている

メビウス帯の大局的トポロジーの意味でのねじれは、具体的に時空点のどこでねじてる、とは定まらない

まるで、真空電磁場の重心みたいです


測地線を２本に分割する双対接続という手法で、メビウス帯のトポロジーを代数的に考察することはできないんでしょうかねえ
http://geometry.mail-box.ne.jp/pdf.bak/09-amari.pdf

大局的トポロジーを考えるにあたっては・・・


統計の基本的なこととして正規分布があります
これを確率分布としたとき、正規分布のようなガウス型分布には必ず期待値があります

一方、統計分布にはもうひとつ変わった特徴を持つコーシー型分布というものがあって、これには期待値はありません
完全ランダムな現象に伴う統計分布だと思われます
真空での（素）粒子の対生成、対消滅などがこのパターンの自然現象だと考えられています

とはいえ、とある自然現象の統計分布は、観測の蓄積によって、規則性がみられることがわかっています
それが物理法則であり、期待値が分かると、未来が確率的に計算予測できる、つまりこれは量子力学です

自然界（宇宙）の統計分布の規格化空間を外の拡大空間から見たとき、サインカーブが延々と続くような分布が得られそうです
この拡張した統計分布から、大局的トポロジーは考察できるかもしれないとわたしなどは思います

宇宙は現状では外から観測できませんが、接続係数の評価で、中にから全体の特徴がわかることがある
中からわかる例としては、幾何のフラクタル図形もそうですね

別コミュにて、メビウストーラスのおもしろいGIFを教わりました
http://curvebank.calstatela.edu/moebius2/moebius2.htm

リーマン幾何学はユークリッド幾何学を一般化した純粋数学です

一般相対論では、真空中の光速ｃに時間を掛けた長さの座標ｃｔ座標を追加して、四元時空のリーマン幾何モデルすなわち擬リーマン多様体を構成します

擬リーマン空間はミンコフスキー空間（x,y,z,-ｃt）のことですよね

単なる空間と多様体は違いますが
リーマン空間に接空間としてミンコフスキー空間を導入した擬リーマン多様体はローレンツ多様体といいます

このようにして得られたローレンツ多様体に、等価原理を適用して得られる局所座標系（局所慣性系）は、接続係数（つまり重力）が０です
純粋なリーマン幾何の接続係数が０であることで、自動的に一般相対論（ローレンツ多様体モデルの理論）で定義される局所慣性系なるものが得られるわけではありません
特に４つ目のｃｔ座標が特殊で、符号反転している点でもノーマルなリーマン空間やリーマン多様体とは異なっています

＞とても勉強になりました。

同感です

岡部先生の「座標変換」は、わたしも読ませていただいていますが
読みやすくわたしにはとても勉強になると自分ではそう思っています


ちなみに
ひょっとしたら、疑問の答えは、リーマン曲率テンソルが０であることに関係しませんかね

リーマン多様体のある領域がユークリッド空間である必要十分条件はリーマン曲率テンソルが0
https://ja.wikipedia.org/wiki/%E3%83%AA%E3%83%BC%E3%83%9E%E3%83%B3%E6%9B%B2%E7%8E%87%E3%83%86%E3%83%B3%E3%82%BD%E3%83%AB#.E3.83.AA.E3.83.BC.E3.83.9E.E3.83.B3.E5.A4.9A.E6.A7.98.E4.BD.93.E3.81.AE.E3.81.82.E3.82.8B.E9.A0.98.E5.9F.9F.E3.81.8C.E3.83.A6.E3.83.BC.E3.82.AF.E3.83.AA.E3.83.83.E3.83.89.E7.A9.BA.E9.96.93.E3.81.A7.E3.81.82.E3.82.8B.E5.BF.85.E8.A6.81.E5.8D.81.E5.88.86.E6.9D.A1.E4.BB.B6.E3.81.AF.E3.83.AA.E3.83.BC.E3.83.9E.E3.83.B3.E6.9B.B2.E7.8E.87.E3.83.86.E3.83.B3.E3.82.BD.E3.83.AB.E3.81.8C0

ある領域における基本計量テンソル gij(x) を全部定数にする座標変換が存在する ⇔ その領域においてクリストッフェル記号を全て0にする座標変換が存在する

とのことらしいでが・・・

計量テンソルは行列の作法によって計算する
接続係数も、計量テンソルで表せるので同様ですね

つまり、接続係数の行列演算が0になる可能性は、計量テンソル（の定義）によって決まる
おそらく、計量テンソルの対称性や、固有値などが関係するはずです

一般には、接続係数は、双対基底の偏微分の計算になるわけですから、接続係数が0となる必要十分条件の証明は大変でしょう

局所慣性系や計量テンソルの定義に従えば、、接続係数が0になるのはほとんどあたりまえです

ただの雑談ですが

非可換代数であっても線形代数ならば解析可能
でも、非線形な非可換代数となると解析的な取り扱いは一筋縄ではいかなくなりますよねえ

線形代数の範囲内で計算可能な局所慣性系は別として
非線形で非可換な偏微分代数式であるアインシュタイン方程式の計算は、一般には数値解析が主体であり、解析的に解ける例はごく限られているかと思います

例えば、回転する質点系に伴う重力場のカー解などは厳密解が得られた希少例です

>>[27]


何度読んでも疑問点がどうも伝わらないため回答になっていないかもしれませんが、
一つ一つお答えしてみますと、

>接続係数を、計量テンソル以外で書き下すことも出来るものなんでしょうかね。

出来ないと思います。

>クリストッフエル記号が0であれば局所慣性係になる、と言うのが物理的な解釈

そうなのでしょうか。
直交座標系（デカルト座標系）での局所慣性係や平坦な時空では
確かにクリストッフェル記号の全成分が0になりますが、
極座標系で表現した場合は非0成分も現れるようです。

>リーマン幾何に戻って、「接続係数」が０となる「必要十分条件」というのはなんなのでしょうか？

直交座標系で表現された「平坦な時空」や「歪みのない多様体」だけではないでしょうか。
接続係数（クリストッフェル記号）の全成分が0になる状況というのはそうそうない気がします。
極座標表現での平坦2次元面や平坦3次元空間でさえ0にはなりませんよね。（非0成分が現れる）

以下に少しまとめてみました。（あくまで極座標表記での話です）

・平坦2次元面や平坦3次元空間
クリストッフェル記号≠0　リッチテンソル＝0　リッチスカラー曲率＝0　リーマンテンソル＝0

・円筒面や円錐面など
クリストッフェル記号≠0　リッチテンソル＝0　リッチスカラー曲率＝0　リーマンテンソル＝0

・2次元球面、3次元球面、ロバートソンウォーカー時空
クリストッフェル記号≠0　リッチテンソル≠0　リッチスカラー曲率≠0　リーマンテンソル≠0

・局所慣性係＆平坦時空
クリストッフェル記号≠0　リッチテンソル＝0　リッチスカラー曲率＝0　リーマンテンソル＝0

・シュヴァルツシルト時空
クリストッフェル記号≠0　リッチテンソル＝0　リッチスカラー曲率＝0　リーマンテンソル≠0

＞なにかの参考になればいいのですが

わたしにとってで恐縮ですが
おもしろい話題と、ご教示を、ありがとうございます

疑問について、正面から解決を目指されているところなどは、まさに自然科学を学ぶものの態度で、見習いたいと思います

とくにご指摘の


　　　　　　微分形式


これは興味深いものですね
そうこう調べているうちに、知見が広がりますよね

漠然とした落書きばかりで気が引けますが

同一のユークリッド空間に張られた直交座標と極座標は、そもそも異質な座標系です
例えば、ユークリド空間の一般化座標をリーマン幾何で考察し、あとで座標変換することで、トポロジカルな考察を一般化することができないかと思いました

これは解析力学による一般相対論の記述にあたるのかもしれません

>>[31]

私も、もう一度確認しました。

（計算したわけではなくて本でカンニングですが）


確かに、全成分＝０にはなってませんね。

あれれ？。(^^;)


でも球面の場合には、添え字によってはθ＝π/２に対してゼロになりますね。

球面状にある接ベクトルの世界に「限定すれば」これが慣性系ということなのでしょうか。

確かに法線方向に飛び出したらビックリポンです。（もう古いなあ）

もう少し考えてみます。

宇宙空間のトポロジーは不明ですが・・・

現状の一般的宇宙モデルとしては、各点で等方的に加速膨張する平坦な時空の各点にミンコフスキー時空が埋め込まれたローレンツ多様体が一般相対論の宇宙空間（真空）を表す動的な時空でしょう

さまざまな物理（力学）の計算では便宜上極座標が使われたりもしますけれど
平坦かつ等方的な加速膨張宇宙なら、

　　　　唯一の原点を持つ極座標ではなく、

もっとも原始的に想起する宇宙の形状は、平坦かつ等方的なユークリッド空間です

重力場の等ポテンシャル面のような極座標計量は、質点まわりのアインシュタイン方程式の静的な解として求めるまでもなくよく知られた単純なものですが、ミンコフスキー時空や直交座標からみたら曲がってますし、重力場の計量なので当然ながら接続係数は０になりません
ただし、重力場にあっても局所慣性系は成り立つし、質点から十分遠方ではほぼ平坦なミンコフスキー時空です

また、局所慣性系の計量は、極座標計量の微小領域と近似的に等しいとみなし得る
地上のレールの上を走る電車は近似的に真っすぐ走ると言いますけど、厳密には地表球面上で真っすぐ走るとは大円軌道を走っていることなわけです
ただ、ユークリッド空間のトポロジー的性質として、、大円に平行な大円は存在しない
つまり、地上を大円に沿って真っすぐ互いに平行に走る２つ以上の電車は厳密には存在しないということになります
宇宙は擬リーマン多様体でモデル化しているので

　　　トーラス

のように（球での大円に相当する軌道として）互いに平行な２直線が存在する可能性もあり得るかと思われます
メビウス帯はトーラスの延長線上にある宇宙の大域的なトポロジーに関する候補モデルのひとつです

一般相対論ではローレンツ多様体の時空座標各点の曲率の変化の様子を計量として算出します
ローレンツ多様体のさまざまな計量についての考察は、リーマン幾何学そのものではなく、一般相対論の微分幾何学的考察ですね

アインシュタイン方程式は非線形方程式なので、一般解のような公式はありませんが例えば
大域的に、全方向に平坦ではなく球対称な（球面座標計量の）ローレンツ多様体（シンプルな丸い平坦な静的宇宙モデル）を仮定した場合
ひとつの質点のアインシュタイン方程式には、厳密解（シュバルツシルド計量）が得られます
こういう話は局所慣性系とは関係なく、シュバルツシルド解はアインシュタイン方程式が厳密に解けるように静的な宇宙の大域的な形（ローレンツ多様体）が簡単設定されている例です

現在、宇宙物理学において宇宙を考察する場合は、アインシュタイン方程式に人工的な宇宙項が付加されたアインシュタインの宇宙方程式によって表されます
ただ、現在の宇宙方程式はアインシュタインが当初想定していた静的な宇宙ではなく、動的な流体型の宇宙（ΛCDMモデル）という設定になっています
加速膨張する動的宇宙のローレンツ多様体の計量（メトリック）はロバートソンウォーカー計量と呼ばれています

このような動的な宇宙の流体モデルは、フリードマン方程式によってニュートン力学に結び付けて考えることができると考えられています

ユークリッド空間にはる座標について、直交座標でないものとして、曲座標や斜交座標を選んでも、ユークリド空間の各点と座標とは一対一に対応する

リーマン幾何の特別な一形態がユークリッド空間ですから
ユークリッド空間の曲座標や斜交座標の性質あるいは座標変換はリーマン幾何でも記述されます

ユークリッド空間にはられた曲座標の中においては、極座標や球面座標は、ガウス曲率によって考察できます
ガウス曲率は、ユークリド空間内の任意曲面を考察する微分幾何学で重要となる考え方で、リーマン幾何学以前の曲面に対する考え方です
リーマン幾何では、曲率以外に、斜交座標に見られる基底の変化（双対基底）にも自由度を拡げている点でユークリッド曲面の考察とは異なります
つまりリーマン曲率を持つ非ユークリッド幾何学的曲面は双対基底の自由度において、ユークリッド空間からはみ出し、歪みます

一般相対論におけるミンコフスキー時空やローレンツ多様体（の大域的なメトリックのもたらす空間）は、４次元の非ユークリッド幾何学的（曲面）時空なので、ユークリッド空間とは様相が相当に異なる概念です

リーマン幾何はリーマン幾何できっちりと基礎を把握してから、物理数学の擬リーマン空間であるミンコフスキー時空や

　　　　擬リーマン多様体

であるローレンツ多様体を考えないと
特殊相対論（局所慣性系）あるいは平坦なミンコフスキー時空において

　　接続係数が０となる条件

のことに、ローレンツ多様体の特別なケースのシュバルツシルド計量とか言い出したら、はあ？みたいなことになりそうですｗ



純数学的な三次元リーマン空間と物理数学的なミンコフスキー時空（四元時空）において、接続係数が０となる条件はどういう違いがあるのか

三次元リーマン空間は四次元ユークリッド空間に置き換えられないのか

ユークリッド空間中でガウス曲率を持つ曲面の＋１次元の超曲面をユークリッド微分幾何の中で考えることと、非ユークリッド幾何学’の空間のリーマン曲率）はどう違うのかという視点もあるかな

リーマン曲率テンソル
https://ja.wikipedia.org/wiki/%E3%83%AA%E3%83%BC%E3%83%9E%E3%83%B3%E6%9B%B2%E7%8E%87%E3%83%86%E3%83%B3%E3%82%BD%E3%83%AB

＞ゲージ変換理論の元になったもののようですが歴史的には重力理論と電磁気学の統一には上手くいかなかったようです


ワイルによる統一場理論
http://members3.jcom.home.ne.jp/nososnd/grel/wunifr.pdf
ここにそういうことが書いてある
だから、それがいままでの文脈に何の関係があるのかは、さっぱりわかりませんけどｗ



＞極座標表現での平坦2次元面や平坦3次元空間でさえ0にはなりませんよね。（非0成分が現れる）

これ、そのものの意味くらいはわかりますがw

局所慣性係の接続係数が０となる条件にとって
これを例示する意味について
何が言いたいのか、どういうつながりがあるのか
どなたかわかりますかね

これだと空間や時空に対して曲がった座標を仮定してるわけでしょ
一般相対論やリーマン幾何学ってのは、誰かが勝手に設定した座標と、時空の測地線と、のすり合わせで接続係数なんてことを議論するものではないですよ
こういう意味での極座標なんて空間や多様体の接続係数うんぬんとは関係ないです
時空そのものがある点に対して球対称な形なら、時空の座標も極座標のようになるけれど、そんな曲がっているものはもちろん接続係数が0にはならない
リーマン幾何の文脈では、局所慣性系のようなユークリッド空間の座標は極座標ではなく、直交座標です

力学で、わざわざユークリッド空間のいたるところ真っすぐで平坦な測地線（あるいは直線的なユークリッド距離計量）に対して曲がった座標を設定するのは、運動方程式が解きやすくなるからです
ただ一般相対論でも、非線形方程式は一般に解けないですから、計算の便宜上、
シュバルツシルド計量のように多様体の形について球対称をはなから仮定してしまうことはあります
シュバルツシルド計量の擬リーマン多様体について、座標というときは、その多様体の測地線に沿った座標を意味します
シュバルツシルド計量の時空の形は球対称というお約束なんで、まったくもってこの座標の大域的性質は局所慣性系と同じものではないが、”球の原点から無限遠では近似的に”ユークリッド空間と同様になります
さらに、球対称な連続的時空多様体の場合、時空各点の近傍系に微小な接空間（微分速度ベクトル空間）が定義できて、それがユークリッド的になっているように定義できます
もちろん、ユークリッド性が数理的に必然されるようなことではありませんよ


根本的に、アインシュタインの一般相対論というのは、時空多様体の幾何学的計算をするものです
ワイル幾何学ってのも
時空多様体の測地線に対して、人間が勝手に持ち込んだような曲がった座標を張り巡らせてどう計算するかと言う議論ではありません
詳細は先のPDFでも参考にすればいいかと思います

一般相対論で、極座標だのなんだのと座標種類の違いに影響されないように一般化座標での考察がしたいなら、すでに落書きしたとも思いますが、解析力学で一般相対論を構成するのが筋でしょう

局所慣性係の接続係数が０となる条件を知りたいというなら
わざわざ時空多様体に、その測地線に対して曲がっているような座標を重ねて考えるのではなく
単に擬リーマン空間や擬リーマン多様体の測地線に合わせて
アフィン接続がどうたらを考察すべき
http://members3.jcom.home.ne.jp/nososnd/grel/affin.pdf

つまり、局所慣性係の接続係数が０となる条件にとって
擬リーマン多様体（ユークリッド計量を含む）に対してそこに極座標などの自分勝手な座標を置いて考えるなんてまったくお門違いな議論です
強いて言うなら、リーマン多様体のことで座標と言うときはその多様体の接空間や大域的な測地線あるいは距離計量に対して曲がっていない座標を選んだと思っておけばいいだけであり、その擬リーマン多様体の接空間や大域的な測地線の計量によって定まる４次元的幾何形状が、その多様体の座標の形なわけです

座標の種類の違いは、基底の取り方の違いです

基底の取り方は任意なので、特定の基底で多様体の性質（歪み）を表現するのは一般化した記述法ではない

そこで、非座標基底という一般基底を用いた接ベクトル空間の定式化が考察されています
非座標基底のアプローチは内山龍雄さんの


　　　　　　　不変変分論


からの進展だと思います


電磁場にフレミングの法則による力が生じる

これは端的に言うと、３次元空間の接ベクトル場において、２つのベクトルの作用によって、この２つのベクトルを含む２次元平面に直交する向きにあらたなベクトルが創発される
２つのベクトルの作用は、それらに直交するひとつのベクトルと等価である（これは超伝導ゼロス解釈による”ホログラフィック原理”の一種と思われる）
この類推から、非座標基底を用いた解析力学による一般相対論の構成は、時空多様体をゲージ場とみたときに時空に重力という力が生じることを説明するのに適するのではないかと思われます
リーマン幾何学の範疇かどうかわかりませんが、非座標基底の非ユークリッド幾何学によって時空多様体を考察すれば、電磁場と重力場の関係性が明確になり、理論物理学としてはむしろこのようなアプローチのほうが本論であるように思えます


詳細はネットで見れませんでしたが、非座標基底を用いた考察としては

非座標基底を用いての重力方程式系の構成　岩永則城
http://gazo.dl.itc.u-tokyo.ac.jp/gakui/cgi-bin/gazo.cgi?no=112139

リーマン接続では、接空間内でベクトルを平行移動させるだけで、ベクトルの大きさは変化しない
ワイル接続では、平行移動するベクトルが大きさを変えるようなケースを考察できるように、リーマン接続に拡縮の係数行列を与えている

双対基底は基底が２つの基底に分裂するとしたものですが、その分裂の詳細は、双対基底のなす角と基底の大きさの２種類の変動の自由度があってなかなか複雑なものです
一般の双対分裂を一意的に表すにはどうすればいいのか、というときはワイル接続のようなアプローチが求められるかなと思います

ユークリッド空間すなわち（局所）慣性系では、そもそも分裂した双対基底というものを考える必要がないので、このような議論は不要ですが、
非ユークリッド空間がユークリッド空間となる条件として
空間の各点すべてにおいて、分裂した双対基底が縮退して、同一のユークリッド空間の基底、になるための条件は、双対基底のなす角と基底の大きさの２種類の変動の自由度を独立させて考察するほうが厳密になるでしょうね

＞極座標表現での平坦2次元面や平坦3次元空間

　　　　↑
この極座標表現てなんやねん、ということよ

極座標表現での平坦2次元面て、そんなもの平坦じゃないんだよ
上のコメントはずいぶんとおかしな言い回しではないですか？



質点の重力場の等ポテンシャル面はユークリッド空間上で曲がった極座標ですが
ニュートン力学は、地球の重力場を平行重力場（ユークリッド空間または直交座標）に近似して地上でみられる物理現象（物体の運動）を法則化している

しかし、リーマン幾何では、曲がっているものを平坦なものに近似したりしませんよ
そんなことをしたら本末転倒ですね


では、リーマン幾何をどう物理学で利用するのかというと
一般相対論では、擬リーマン空間から”擬リーマン多様体”を構成するとき

空間各点の近傍に

空間の計量（大域的な計量）Aとは異なる計量Bを導入するのです

局所的にはその計量Bを用いた特殊相対論的なニュートン力学が成り立つ部分空間が想定できます
これは空間の微小な各点にでもなったような立場です
宇宙空間の時空多様体モデルを概観するときは大域的な計量Aを用いますが、無限遠では計量Aは計量Bに近似的に等しくなります


　　　　　　　一般相対論は”多様体”の理論です

ニュートン力学は近似的ユークリッド”空間”と絶対時間に基づく理論で

相対論は、擬リーマン”時空”多様体の理論

という違いがあります
これはリーマン幾何には縁もゆかりもないが物理学の基本です

＞次に、

（わたしのコメント）
一般相対論で、極座標だのなんだのと座標種類の違いに影響されないように一般化座標での考察がしたいなら、すでに落書きしたとも思いますが、解析力学で一般相対論を構成するのが筋でしょう

（対してあなたの）
＞ニュートン力学で自由粒子の運動方程式を作用積分として書き下し、それを共変化して、オイラーラグランジュ方程式に直接代入すると、そこから得られるのは、コメント[9]で示された測地線の方程式になります。 要するに一般化座標を取っても結論は変わりません。まぁ当たり前ですが・・・


＞一般化座標を取っても結論は変わりません。まぁ当たり前ですが・・・

結論は変わりませんてｗ

いまの文脈において、あたりまえなんかではないですよ
物理ではなにゆえに、結論は変わらないのに運動方程式と同等なラグランジアンによってニュートン力学を解析力学で運動方程式を解析的に扱うのかわかってますか？

【43】のわたしの落書きで並べた科学の専門用語をご自分で調べられたほうがいいかなと思いますね
ポイントは基底です
ニュートン力学の運動方程式と等価なラグランジアンを用いた解析力学は、一般化座標という基底が不明な相対距離だけに依存する相空間で記述され、相空間では運動量も座標として扱います
対してリーマン幾何は特定の基底を選んで接続係数を考察している幾何であり、リーマン幾何の基底の基準はユークリッド空間の基底です

数学的な空間や多様体は、

　　人間の知覚認識ライクな幾何にそのままイコールではありません

物理の相空間や時空やヒルベルト空間もみんなそうです

＞「局所」ですから、曲がった空間であっても微分して極値をとれれば、その点では慣性系が取れるものと考えるできではないでしょうか。 おおざっぱに言うと、この微分可能性が保証されているものがリーマン空間であろうと考えます。 「接続係数」と「曲率」をごちゃ混ぜにしているように思います。

わたしは、物理を論じる一般相対論は”擬リーマン多様体”を時空モデルに採用した理論だといってるのです
幾何的量の微分可能性など、物理法則ではありません

物理の擬リーマン多様体で局所的なユークリッド的接空間をおいていいかどうかは、観測事実に基づく妥当性です
微分可能だからどうということは数学的な多様体の構成のメカニズムの話です
物理と数学をごっちゃにしているのがあなたなんだと思います

＞ひょっとして私の発言がミスリードしてしまったのかと

いやいや、その心配はわたしには無用ですよ
あなたのリードにそって考えることも
物理を教わることも
なさそうなので（笑

わたしとしては、このように、どなたかがいろいろ書いてくれると
それをもとに自分の勉強になるんで
なんでも躊躇せず、思うところを書いてくださったらわたしはうれしいかぎりです


＞貴殿のコメントは修辞的な文言が多く・・・

科学の単語を適切に表現しているつもりですが、疑問や間違ってるんじゃないかと思うところがあれば

まず、聞いてください

わたしの理解の範囲で説明したいと思います


＞毎度、ご教示頂きありがとうございます

いや、わたしのコメントを教示だとは申しません

わたしのは落書きです

しかし、言い分は、物などの理や筋を自分で可能な限りに重視しております
もちろん数学を応用する部分に関しては数学的計算や証明をおろそかには考えておりません
誤解なきよういただけたら幸いです

＞言わば、２次元球面を「時空そのもの」のモデルとして仮定しているのです。 これは単純すぎるモデルですが、「測地線」に関しては極座標に戻ることで「見やすい」からです。 ガウスは「ガウス曲率」を見出した時、「真に驚嘆するべき定理」と言ったそうです。 「空間や時空に対して曲がった座標を仮定している」ぐらいの思い付きで、これほど大数学者が驚くとは思えないですよね？。

　　【局所慣性系の接続係数が0になる】

かどうかの考察において、こういう話をする必要はなく
一般相対論のシュバルツシルド座標とか持ち出すなら
このような大域的な時空の曲率が問題になります

数学上の多様体を理解されることで、非ユークリッド空間の大域的トポロジーと接空間の計量の違いが判るかと思います

ひょっとしたら、あなたたちは大域的な計量と局所座標系の計量をごっちゃにしているのですかね


＞「測地線」に関しては極座標に戻ることで「見やすい」からです

見やすいって誰がですか？
あなたかな（笑
わたしなら、測地線なんてさまざまに歪むんですから、極座標で見やすいなんてとうてい理解不能ですよ

極座標の住人が直線を見たら”曲線”になります

ただしユークリッド空間内で球面な地上に立っている人間は極座標の住人ではなく
人間はまっすぐな基底のユークリッド空間の住人として等方的な地上に立つという前提で物理学は成り立っています
なのでGPSの測位システムでは標高に対する補正が別途必要になります

極座標の球面上の最短距離は球面に沿った測地線の距離で定義された線です
極座標に対して直交座標の基底は曲がっているのです
ある立場での”直線”つまり最短距離がどんな座標でも直線だということにはなりません
ある座標での別な基底の座標からみると
最短距離が延びるときはまだしも湾曲でイメージできますが
　　
　　縮むときもある

ので、ガウスの曲面論では不十分です
つまり空間の曲率っていうのは、正負のような２方向の自由度があって、ユークリッド空間内の曲面の曲率がすべてでもない
これは非ユークリッド幾何学や現代の微分幾何の常識です


＞これほど大数学者が驚くとは思えないですよね？

（Wikiより）
https://ja.wikipedia.org/wiki/%E9%A9%9A%E7%95%B0%E3%81%AE%E5%AE%9A%E7%90%86

この定理が「驚異」的である理由は、後述するようにガウス曲率の定義は空間内における曲面の外在的な情報（曲面に直交する法ベクトル）を使用しているにも関わらず、最終的にはガウス曲率は空間内への埋め込みに関する外在的な情報を必要とせず、内在的な量のみで求められることである。曲面の「曲がり具合」を表すガウス曲率が曲面の内在量であるという事実は、


　　　【空間の「曲がり具合」を考察するのに「外の世界」の情報が必要でない】


可能性を示唆し、後のリーマン幾何学、そしてリーマン幾何学を数学的基礎として構築された一般相対性理論へ繋がることとなる。
証明には、ガウス曲率の定義とリーマン曲率テンソルに関するガウス・コダッチ方程式（英語版）を用いる方法などがある。
なお、曲面のガウス曲率は、局所等長写像に関して不変である。
＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿

つまり、井の中の蛙が外の世界を知るすべを持てるんじゃないかということから、驚愕と言われます

２次元球面の各点は
２次元平面の各点と同様に
面内のあらゆる方向（３６０度）について”等方的”かつ”定曲率”の不変な基底を持ちます
３次元ユークリッド空間の中で、球面の大円は当然ながら曲線ですが、0を定数と同一視したら、直線も大円も曲率の値は同じようにいたるところで一定値です
これをもって３次元空間の住人が２次元球面を平坦だとは言わないでしょうけど
球面内の２次元人たちは平坦だと認識しているはずですね
この見解の相違は

　　　　　”次元の違い”

にもよるのであって、内的な曲率だけの話ではないです
いたるところ定曲率でない場合は、基底の接続という概念によって、次元に関係なく、空間の歪みといか様相の考察が可能になります
ただ、球面をユークリッド空間のように等方的に３次元化したと思ったとき、つまり

　　　３次元球面空間

というべき仮想的空間を考えたとき、空間の中にいては、ユークリッド空間と３次元球面空間どちらの空間においても各点は全く対等で個性がなく、ユークリッド空間と３次元球面空間は区別できないでしょう
不変性を保ったまま平行移動が自由に行えるユークリッド空間やｎ次元球面空間では曲率の値はスカラーでありその値は0であろうとなんであろうと一定不変であり曲率に特別な意味はありません
0と有限数値を同様な定数と仮定したら、直線と円は定曲率という同じ性質の数学的対象にすぎなくなるが、0を特異点とみたら、直線は特異線とでも言えるのかもしれませんが

対して、一般の曲線は曲率（曲率の定義はともかくとしてもそれ）が場所の関数になります
同様の考察で、一般に接続係数（接続係数の定義はともかくとしてもそれ）が0でないような空間の各点は、個性が定まってしまいます
つまり、ある特定の点の基底は、その点の周辺のすべての（立体的あるいは高次元的な）方向に隣接する各点（ある特定の点を包み込むあるいは原点とする微小球面内の点）の基底との相対曲率の分布が”非等方的”であり、”曲率の変化”の空間分布に関する個性があります
この個性をどのような超空間でみたとしても、不変的な量で評価することができるのではないかと思います
その不変量をもとに任意に選んだ２点間距離をユークリッド空間での長さに翻訳するとどうなるのかという問題はともかくとしてｗ

ちなみに各点に個性のないユークリッド空間であれば
数学では３次元空間では三角法による３点で２点間距離の測定が可能だと考えます
物理学では光速不変に基づく測距であり、時計あわせのために、３次元空間に対しては時間補正用を含めた四点が必要となります
GPSでは、四つの衛星が見えているとき、測距が可能になると考えます

＞これは単純すぎるモデルですが、「測地線」に関しては極座標に戻ることで「見やすい」からです

極座標は原点という１つの点にとって対称性を持つが、他のすべての点の立場では対称性を持たないので、宇宙の幾何構造が備えるべきい性質ではないし、相対性原理にも合致しない

幾何学などの数学は人間の考えに対する論理を追及しているが
一般相対論のような物理学理論では、宇宙の物理現象に見られる法則を観測して、法則を数式で表して未来を計算する

地球や地球に住む人間を中心に考えようという態度に戻ることはもうないです
宇宙の時代です

数学は、物理にとって道具にすぎません


＞さて、私の疑問はもとより解決済みです。

なにがどう解決されたのか知りませんが、礼にはおよびません
なががどのように解決されたのか

質問でもしているつもりなら、それを書くべきです

＞一生懸命考えて下さって、ありがとうございました。

ここでの一連のわたしの落書きは、自分の持論を語ろうとしているのではないし、あなたを説得するものでもなく
物理学や数学の基本的な考え方を口語的に復唱している、といったものが主です


わたしは・・・

その言い方はこうこうこういう理由でおかしいでしょう
というような指摘（や疑問がもしあればわたしに質問を）していただくとか
基本についての他の方のコメントを聞いてみたいんですよ

わたしにとって漠然としたあなたのコメントはそのためのきっかけになることを期待するものです