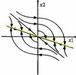
フライバックトランスの動作を見て湧いた疑問です。
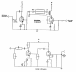
回路図の様に、トランスの一次側に一定時間直流電圧を印加した後、スイッチを切り替えて一次側、二次側共に抵抗を接続した場合、一次側、二次側それぞれの電圧、電流はどういった挙動を示すのか???
単純に連立微分方程式として解けそうな気がしますが、電圧(電流)の初期条件がネックです。
フライバックコンバーターの場合、一次側と二次側は同時に導通しませんのでトランスコア内の磁束の連続条件(等アンペアターンの法則)より簡単に初期条件が求まりますが、この場合はどうなるのでしょう??
暫く考えてみましたが、確証ある答えが出てきません。
是非、皆さんの意見を伺いたいです。
回路図の様に、トランスの一次側に一定時間直流電圧を印加した後、スイッチを切り替えて一次側、二次側共に抵抗を接続した場合、一次側、二次側それぞれの電圧、電流はどういった挙動を示すのか???
単純に連立微分方程式として解けそうな気がしますが、電圧(電流)の初期条件がネックです。
フライバックコンバーターの場合、一次側と二次側は同時に導通しませんのでトランスコア内の磁束の連続条件(等アンペアターンの法則)より簡単に初期条件が求まりますが、この場合はどうなるのでしょう??
暫く考えてみましたが、確証ある答えが出てきません。
是非、皆さんの意見を伺いたいです。
|
|
|
|
コメント(7)
問題の回路でスイッチが上側のときだと、
一次側の電流が無限大の時間で発散してしまいます。
電源に直列に抵抗が必要です。
一次側、二次側の抵抗とインダクタンス、電流をそれぞれ
R1、R2、L1、L2、i1、i2とすると、
スイッチを下側に切り替えた後の電圧方程式は?式になります。
上の式が一次側の電圧方程式、下の式が二次側の電圧方程式です。
二次側の電圧方程式を?式のようにi1について変形して、
一次側の電圧方程式に代入してi1を消去すると?式になります。
i2の1回微分の項の係数が0でない、つまりL1 * L2 = M^2でない、
変圧器が密結合でないとしてi2の分母を払うと?式になり、
i2を電荷qの時間微分に置き換えて各係数をAとBで置き換えると
?式になります。
ここまで変形しなくても途中で分かりますが、
RLC直列回路と同じ形の式で、2階の微分方程式です。
つまり、電荷や電流はRLC直列回路のように振動する
可能性があるということです。
これは驚きました。実際に式を変形してみるまで
分かりませんでした。
初期条件ですが、スイッチを下側に切り替えた瞬間をt=0として、
二次側の電流の初期値は0です。もし0でなければ、
スイッチを切り替えた瞬間で電流が不連続になってしまいます。
二次側はスイッチ切り替え前は開放なので、電流は0です。
2階の微分方程式なのでもうひとつ初期条件が必要ですが、
「初期電荷は0」でしょうか?これは自信がありません。
一次側の電流が無限大の時間で発散してしまいます。
電源に直列に抵抗が必要です。
一次側、二次側の抵抗とインダクタンス、電流をそれぞれ
R1、R2、L1、L2、i1、i2とすると、
スイッチを下側に切り替えた後の電圧方程式は?式になります。
上の式が一次側の電圧方程式、下の式が二次側の電圧方程式です。
二次側の電圧方程式を?式のようにi1について変形して、
一次側の電圧方程式に代入してi1を消去すると?式になります。
i2の1回微分の項の係数が0でない、つまりL1 * L2 = M^2でない、
変圧器が密結合でないとしてi2の分母を払うと?式になり、
i2を電荷qの時間微分に置き換えて各係数をAとBで置き換えると
?式になります。
ここまで変形しなくても途中で分かりますが、
RLC直列回路と同じ形の式で、2階の微分方程式です。
つまり、電荷や電流はRLC直列回路のように振動する
可能性があるということです。
これは驚きました。実際に式を変形してみるまで
分かりませんでした。
初期条件ですが、スイッチを下側に切り替えた瞬間をt=0として、
二次側の電流の初期値は0です。もし0でなければ、
スイッチを切り替えた瞬間で電流が不連続になってしまいます。
二次側はスイッチ切り替え前は開放なので、電流は0です。
2階の微分方程式なのでもうひとつ初期条件が必要ですが、
「初期電荷は0」でしょうか?これは自信がありません。
>Denkoさん
レスありがとう御座います。
>電荷や電流はRLC直列回路のように振動する可能性があるということです。
自分も確認してみましたが、トランスが密結合でなく、かつ?式の微分方程式の係数行列の固有値が実数とならない場合、確かに減衰振動を行う可能性がありますね。しかも振動のモードについても一つでないかも知れません。
>初期条件ですが、スイッチを下側に切り替えた瞬間をt=0として、 二次側の電流の初期値は0です。もし0でなければ、スイッチを切り替えた瞬間で電流が不連続になってしまいます。
インダクターにおいて、状態変化前と状態変化後の電流が連続になるのは、一つのコアに対して一つのコイルが巻かれている場合のみではないでしょうか?
この場合、状態変化前後でコア内の磁束が不連続とならないように電流が流れ、その結果磁束を作る媒体である電流も連続となります。これはコアに蓄積された励磁エネルギーの出口が一つしかない為に起こる現象です。
しかしトランスの場合は(特に今回の様な場合は)、励磁エネルギーの出口が二つありますので、磁束が連続となるように電流はΦ(0)=(n1×i1[0])/R'+(n2×i2[0])/R'を満たして流れるはずです。
Φ(0):スイッチ切り替え直前のコア内の磁束
n1,n2:一次側と二次側の巻き数
R':トランスコアの磁気抵抗
この場合、初期値を求めるのにi1[0]とi2[0]の間の関係式が必要となります。
最初はV1/V2=n1/n2の関係に拘束されるのかなと思い、SPICEでシュミレーションしてみましたが、実際に求めた計算結果と合いません。(状態変化点が特異点である事についての影響もあると思いますが・・・)
どうも、トランスに関して詳細に記述した文献が見つからず、実機による実験もままならないため、未だに疑問のままです。
レスありがとう御座います。
>電荷や電流はRLC直列回路のように振動する可能性があるということです。
自分も確認してみましたが、トランスが密結合でなく、かつ?式の微分方程式の係数行列の固有値が実数とならない場合、確かに減衰振動を行う可能性がありますね。しかも振動のモードについても一つでないかも知れません。
>初期条件ですが、スイッチを下側に切り替えた瞬間をt=0として、 二次側の電流の初期値は0です。もし0でなければ、スイッチを切り替えた瞬間で電流が不連続になってしまいます。
インダクターにおいて、状態変化前と状態変化後の電流が連続になるのは、一つのコアに対して一つのコイルが巻かれている場合のみではないでしょうか?
この場合、状態変化前後でコア内の磁束が不連続とならないように電流が流れ、その結果磁束を作る媒体である電流も連続となります。これはコアに蓄積された励磁エネルギーの出口が一つしかない為に起こる現象です。
しかしトランスの場合は(特に今回の様な場合は)、励磁エネルギーの出口が二つありますので、磁束が連続となるように電流はΦ(0)=(n1×i1[0])/R'+(n2×i2[0])/R'を満たして流れるはずです。
Φ(0):スイッチ切り替え直前のコア内の磁束
n1,n2:一次側と二次側の巻き数
R':トランスコアの磁気抵抗
この場合、初期値を求めるのにi1[0]とi2[0]の間の関係式が必要となります。
最初はV1/V2=n1/n2の関係に拘束されるのかなと思い、SPICEでシュミレーションしてみましたが、実際に求めた計算結果と合いません。(状態変化点が特異点である事についての影響もあると思いますが・・・)
どうも、トランスに関して詳細に記述した文献が見つからず、実機による実験もままならないため、未だに疑問のままです。
- mixiユーザー
- ログインしてコメントしよう!
|
|
|
|
電子回路理論研究会 更新情報
-
最新のアンケート
-
まだ何もありません
-