- 詳細 2016年10月30日 03:02更新
-
従来の数の概念
自然数⇒実数(X)⇒虚数(Y)⇒時数(Z)⇒複素数(X.Y)
とすると新たなるZ軸というものが考えられます。
それを時数(Z)として3次元空間的な数字の概念・複時数(X.Y.Z)
を考案しました。
結構単純なので、「この考えが正しいのか?」と思いコミュを作りました。
当方数学は全くの無学者ですので、全然見当違いの事を書いてあるかも
しれません、なにぶんその旨をご了承ください。
とりあえず、概念図と特徴を書いたものをUPしますので、気軽にご意見
いただけたらと思います。
-------------------------------------------------
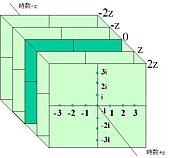
1・「複時数」とは?(実数から複時数までの概念図)
今ある数の概念を次元化すると下記の様に説明できると思う。
自然数:繋がりを持たない連続した数(点=0次元)
実数:実数X軸(線=一次元)0を基準とした繋がりのある連続した数
複素数:実数X軸 虚数Y軸(面=二次元)
次元の認識と数域の認識を共通化させる事により、三次元という考えが
自然に出てくると思うところから複素数と言う数字の平面から
新たな時数という軸を設けることにより複時数という立体としての
数字の空間認識が可能ではないかと考えた。
以上の性質から時数と言うのを立体の特性を踏まえた数字ではないのかと下記の様に定義した。
2・「時数」とは?(新しい軸)
複素数(実数をX軸、虚数をY軸として考える)を二次元平面として位置づけて、時間軸Zを新たに設ける事により、数の概念を3次元化し認識させて具現化するために存在する数である。
?複素数(XY)では表現できない、X軸とZ軸にある数字、複時数(XYZ)とY軸とZ軸にある複時数(XYZ)を認識できる。
?Z軸上の数字としての性質はX軸(実数)とY軸(虚数)と同じだが、時数は観点上2つの性質により、数字の特性を変化させる性質がある。
?数の空間を認識して、基準0(原点または光源)を設ける事により角度や時数平面を変化させる事により数の性質が変わる。
----------------------------------------------------
自然数⇒実数(X)⇒虚数(Y)⇒時数(Z)⇒複素数(X.Y)⇒複時数(X.Y.Z)
複時数:実数X軸 虚数Y軸 時数Z軸(立体=三次元)