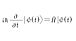- 詳細 2015年11月12日 01:28更新
-
群論の応用がテーマです。
群論そのものよりは、使う群論。
キーワード
group、リー群、リー代数(リー環)、対称性、シンメトリー、表現論、既約表現、ユニタリ表現、回転群、ローレンツ群、U(1)、SU(2)、SU(3)、SU(5)、SO(10)、E(8)、結晶群、数学の他分野(幾何学等)への応用、スピン、スピノル表現、可約表現、単純リー群、変換群、離散群
指標(characters)、ディンキン図形、ルート、ウエイト、
素粒子、バリオン、メソン、クォーク、レプトン、ゲージボソン
対称性の破れ(崩れ)、
ホモトピー群、ホモロジー群、コホモロジー群、被覆群
ラグランジアン
くりこみ、renormalization、くりこみ群
保存則、ネーターの定理
超対称性
非可換ゲージ理論、共変微分
困ったときには