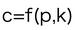この問題中での「約○○」は、
「上から2桁目を四捨五入した時の値が○○」を意味することにします
?日本人女性の平均寿命は86年…って約何秒?
a.約3億秒
b.約30億秒
c.約300億秒
?約30℃の水が約7リットルと、
約70℃の水が約3リットルあります。
混ぜると約何℃になるでしょう?
a.約40℃
b.約50℃
c.約60℃
?7の7の7乗乗÷7の7乗の7乗は約何桁ですか?
a.約70万桁
b.約700万桁
c.約7000万桁
?約5である数が20個あります。
全て足して100に満たない確率は?
a.50%より大きい
b.50%
c.50%より小さい
?バラが1000本必要です。
約200本の花束を5つ用意しても足りない確率は?
a.50%より大きい
b.50%
c.50%より小さい
「上から2桁目を四捨五入した時の値が○○」を意味することにします
?日本人女性の平均寿命は86年…って約何秒?
a.約3億秒
b.約30億秒
c.約300億秒
?約30℃の水が約7リットルと、
約70℃の水が約3リットルあります。
混ぜると約何℃になるでしょう?
a.約40℃
b.約50℃
c.約60℃
?7の7の7乗乗÷7の7乗の7乗は約何桁ですか?
a.約70万桁
b.約700万桁
c.約7000万桁
?約5である数が20個あります。
全て足して100に満たない確率は?
a.50%より大きい
b.50%
c.50%より小さい
?バラが1000本必要です。
約200本の花束を5つ用意しても足りない確率は?
a.50%より大きい
b.50%
c.50%より小さい
|
|
|
|
コメント(18)
(4)について…
「約5」の数nの範囲が
4.5≦n<5.5
と表せるため、
約5である数20個の合計をSとすると、
90≦S<110
と表される。
ここで答えるべき確率は、
S<100
の範囲に収まる確率だが、
90≦S<100 ←求める事象
100≦S<110 ←余事象
と分断できるため、
(4)の正解はb。
(5)については基本的に同様に考えるが、
本数なので"整数値"しか取らない。
これを踏まえると、合計本数Sの範囲は
750≦S≦1245
∴ 750≦S≦999 ←求める事象
1000≦S≦1245 ←余事象
正解はa。
あと些細な事ながら気になったのですが、
地球の公転周期は365.2422(日)だと思います…。
「約5」の数nの範囲が
4.5≦n<5.5
と表せるため、
約5である数20個の合計をSとすると、
90≦S<110
と表される。
ここで答えるべき確率は、
S<100
の範囲に収まる確率だが、
90≦S<100 ←求める事象
100≦S<110 ←余事象
と分断できるため、
(4)の正解はb。
(5)については基本的に同様に考えるが、
本数なので"整数値"しか取らない。
これを踏まえると、合計本数Sの範囲は
750≦S≦1245
∴ 750≦S≦999 ←求める事象
1000≦S≦1245 ←余事象
正解はa。
あと些細な事ながら気になったのですが、
地球の公転周期は365.2422(日)だと思います…。
初カキコです。よろしくおねがいしまーす。
4ですけど答えは(C)で
Namiyoshiさんに付け加える形になるんですが、これにそれぞれの確率を付け加えて考えると90≦S<110の間でそれぞれの値になりうる組み合わせの数をグラフで表すと100を頂点とした山の形をしたグラフになります。
そのうえで考えると100になる組み合わせの数をx、90〜110の間で考えられる値の数を2Yと置くと
90≦S<100の範囲での組み合わせの総数は{1+(X-1)}*Y/2
100≦S<110 の範囲での組み合わせの総数は(X+1)*Y/2
になるため、若干ですが100以上になる確率のほうが大きいためCになると考えました。
わかりにくい文章で申し訳ないm(_)m
4ですけど答えは(C)で
Namiyoshiさんに付け加える形になるんですが、これにそれぞれの確率を付け加えて考えると90≦S<110の間でそれぞれの値になりうる組み合わせの数をグラフで表すと100を頂点とした山の形をしたグラフになります。
そのうえで考えると100になる組み合わせの数をx、90〜110の間で考えられる値の数を2Yと置くと
90≦S<100の範囲での組み合わせの総数は{1+(X-1)}*Y/2
100≦S<110 の範囲での組み合わせの総数は(X+1)*Y/2
になるため、若干ですが100以上になる確率のほうが大きいためCになると考えました。
わかりにくい文章で申し訳ないm(_)m
>xevsさん
>その値xの存在を仮定して議論することはできません…
んー確かに実数は無限にはあるんですが、存在する具体的な個数としてXが出てこなくても、存在確率の最大値をXとおくことはできるのではないかと思うんですが…
私は単純に、さいころ二つの和が2〜12の間になる場合最も7の出る確率が高くなるってところから考えていきました。
これから、個々の値の存在確率は要因が無限にあろうとも一番出現率が高いところ(この問の場合では中心の100の地点)を中心にした凸形のグラフになるんではないかと考え、そこの地点の存在確率をXと起きました。
こういう考え方だとXを定義できるのではないかとおもったのですがいかがでしょうか?
>その値xの存在を仮定して議論することはできません…
んー確かに実数は無限にはあるんですが、存在する具体的な個数としてXが出てこなくても、存在確率の最大値をXとおくことはできるのではないかと思うんですが…
私は単純に、さいころ二つの和が2〜12の間になる場合最も7の出る確率が高くなるってところから考えていきました。
これから、個々の値の存在確率は要因が無限にあろうとも一番出現率が高いところ(この問の場合では中心の100の地点)を中心にした凸形のグラフになるんではないかと考え、そこの地点の存在確率をXと起きました。
こういう考え方だとXを定義できるのではないかとおもったのですがいかがでしょうか?
やはり、手を抜くと失敗しますね。
(4)について、
約5である数nについて、
4.5≦n<5
5≦n<5.5
この2範囲に入る確率はそれぞれ50%と考えられます。
ここで、「約5である数a,b」の和について、
9≦a+b<10 ─α
10≦a+b<11 ─β
それぞれの範囲に入る確率を考えます。
a=5であるとき、
9.5≦a+b<10
10≦a+b<10.5
この2範囲に入る確率はそれぞれ50%になるため、
α50%、β50%ということになります。
同様に、a=5を中心にした4.5<a<5.5の範囲であれば、
α50%、β50%と言えます。
なぜなら、4.5<a<5におけるα、βの確率は、
5<a<5.5におけるα、βの確率のちょうど逆になるためです。
a=4.5の場合はα100%、β0%ですので、
aが想定しうる全範囲(4.5≦a<5.5)について考慮すると、
僅かながらαがβを上回る、と結論付けることができます。
3数以上であっても同様のことが言えるので、
「約5である数20個の和S」について、
90≦S<100
100≦S<110
それぞれの確率は、上式のほうが僅かに上回り、
解はa、ということになると思います。
(5)についても後ほど検証しなおしてみます。
(4)について、
約5である数nについて、
4.5≦n<5
5≦n<5.5
この2範囲に入る確率はそれぞれ50%と考えられます。
ここで、「約5である数a,b」の和について、
9≦a+b<10 ─α
10≦a+b<11 ─β
それぞれの範囲に入る確率を考えます。
a=5であるとき、
9.5≦a+b<10
10≦a+b<10.5
この2範囲に入る確率はそれぞれ50%になるため、
α50%、β50%ということになります。
同様に、a=5を中心にした4.5<a<5.5の範囲であれば、
α50%、β50%と言えます。
なぜなら、4.5<a<5におけるα、βの確率は、
5<a<5.5におけるα、βの確率のちょうど逆になるためです。
a=4.5の場合はα100%、β0%ですので、
aが想定しうる全範囲(4.5≦a<5.5)について考慮すると、
僅かながらαがβを上回る、と結論付けることができます。
3数以上であっても同様のことが言えるので、
「約5である数20個の和S」について、
90≦S<100
100≦S<110
それぞれの確率は、上式のほうが僅かに上回り、
解はa、ということになると思います。
(5)についても後ほど検証しなおしてみます。
- mixiユーザー
- ログインしてコメントしよう!
|
|
|
|
数理パズル 更新情報
-
最新のイベント
-
まだ何もありません
-
-
最新のアンケート
-
まだ何もありません
-
数理パズルのメンバーはこんなコミュニティにも参加しています
人気コミュニティランキング
- 1位
- 北海道日本ハムファイターズ
- 28044人
- 2位
- 暮らしを楽しむ
- 77094人
- 3位
- 独り言
- 9638人