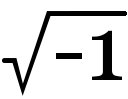ぼくは数学専門でもなんでもないのですが、「リーマン博士の大予想」という素人向けの本を読んでみました。素数の分布の仕方がリーマンにより予想されたが、150年近く証明されていないという話です。そのリーマン予想で、虚数、複素数が重要な役割を果たしています。
そんな虚数ですが、どうもぼくには解せないのです。 学校で勉強する数学 〜たとえば図形の定理、数列、微積分〜 は、なるほど「自然科学」と呼ばれる通り、「もともと存在していたものを発見した」という気がします。 ところが虚数は「発見」という気がしません。 絵や音楽、小説と同様、「人間が創ったもの」、つまり
★虚数は「発明」ではないか
と思います。
上記の本でもこのことは議論されていて、
・Hイワニッチらは「発明」と言い、
・Pサルナックらは「発見。神の贈り物だ」と言い、
・Aイビッチは「発明か発見かは哲学の問題であり、かかわりたくない」
としています。ちなみに、2分の1乗がルートであることや、マイナスの数 x マイナスの数=プラス というのも発明という考え方も紹介されていました。
皆さんのご意見、コメントをいただけるとありがたいです。
虚数は発明か、発見か。はたまた、どっちでもないか。
そんな虚数ですが、どうもぼくには解せないのです。 学校で勉強する数学 〜たとえば図形の定理、数列、微積分〜 は、なるほど「自然科学」と呼ばれる通り、「もともと存在していたものを発見した」という気がします。 ところが虚数は「発見」という気がしません。 絵や音楽、小説と同様、「人間が創ったもの」、つまり
★虚数は「発明」ではないか
と思います。
上記の本でもこのことは議論されていて、
・Hイワニッチらは「発明」と言い、
・Pサルナックらは「発見。神の贈り物だ」と言い、
・Aイビッチは「発明か発見かは哲学の問題であり、かかわりたくない」
としています。ちなみに、2分の1乗がルートであることや、マイナスの数 x マイナスの数=プラス というのも発明という考え方も紹介されていました。
皆さんのご意見、コメントをいただけるとありがたいです。
虚数は発明か、発見か。はたまた、どっちでもないか。
|
|
|
|
コメント(89)
最近、数論の勉強をしています。
たとえばピタゴラスの定理が有りますが、
数を複素数(虚数)まで拡げると、まことにすっきししますね。
ここで、i=√(-1)
z^2=(m^2+n^2)^2
=((m+in)*(m-in))^2 ?
={(m+in)*(m+in)}*{(m-in)*(m-in)} ?
={(m^2-n^2)+2imn}*{(m^2-n^2)-2imn}
=(m^2-n^2)^2+(2mn)^2
x=m^2-n^2, y=2mn, z=m^2+n^2
((m+in)(m-in))^2=(m+in)(m+in)(m-in)(m-in)
とかけ算の順番を変えて、
別の答えが出てくるところがおもしろい。
m=2, n=1とすると、
{(2+i)(2-i)}^2=(4+1)^2=5^2
(2+i)^2*(2-i)^2=(3+4i)(3-4i)=3^2+4^2
物理・化学では、分子、原子、素粒子というものを
考えるようですが似ているなと感じています。
ガウスは、数論に複素数をすでに考えていたのだが、
巧妙に波風を立てないように隠していたと、
高木貞治さんの初等整数論講義にありました。
同書には、イデアル論が登場します。
6=2*3=(1+√(-5))(1-√(-5))
21=3*7=(1+2√(-5))(1-2√(-5))=(4+√(-5))(4-√(-5))
について、
2=A^2,1+√(-5)=AB, 1-√(-5)=AB',
3=BB',1+2√(-5)=B'C, 1-2√(-5)=BC'
7=CC',4+√(-5)=BC,4-√(-5)=B'C'
6=(A^2)(BB')=(AB)(AB')
21=(BB')(CC')=(B'C)(BC')=(BC)(B'C')
上の関係は最初、クンマーによって「理想的の数」の理論として組み立てられ、
その後、簡単明瞭にしてかつ一般的な理論としてデデキントが構成することに成功した。かれは理想数にちなんで 「イデアル」と名付けた。
科学の発明は、そこに元から有るものを発見していくという側面が強い
のだと感じます。
たとえばピタゴラスの定理が有りますが、
数を複素数(虚数)まで拡げると、まことにすっきししますね。
ここで、i=√(-1)
z^2=(m^2+n^2)^2
=((m+in)*(m-in))^2 ?
={(m+in)*(m+in)}*{(m-in)*(m-in)} ?
={(m^2-n^2)+2imn}*{(m^2-n^2)-2imn}
=(m^2-n^2)^2+(2mn)^2
x=m^2-n^2, y=2mn, z=m^2+n^2
((m+in)(m-in))^2=(m+in)(m+in)(m-in)(m-in)
とかけ算の順番を変えて、
別の答えが出てくるところがおもしろい。
m=2, n=1とすると、
{(2+i)(2-i)}^2=(4+1)^2=5^2
(2+i)^2*(2-i)^2=(3+4i)(3-4i)=3^2+4^2
物理・化学では、分子、原子、素粒子というものを
考えるようですが似ているなと感じています。
ガウスは、数論に複素数をすでに考えていたのだが、
巧妙に波風を立てないように隠していたと、
高木貞治さんの初等整数論講義にありました。
同書には、イデアル論が登場します。
6=2*3=(1+√(-5))(1-√(-5))
21=3*7=(1+2√(-5))(1-2√(-5))=(4+√(-5))(4-√(-5))
について、
2=A^2,1+√(-5)=AB, 1-√(-5)=AB',
3=BB',1+2√(-5)=B'C, 1-2√(-5)=BC'
7=CC',4+√(-5)=BC,4-√(-5)=B'C'
6=(A^2)(BB')=(AB)(AB')
21=(BB')(CC')=(B'C)(BC')=(BC)(B'C')
上の関係は最初、クンマーによって「理想的の数」の理論として組み立てられ、
その後、簡単明瞭にしてかつ一般的な理論としてデデキントが構成することに成功した。かれは理想数にちなんで 「イデアル」と名付けた。
科学の発明は、そこに元から有るものを発見していくという側面が強い
のだと感じます。
>一方、ラジアン表現で書くと、
>cos(π/2) + i sin(π/2) = i
>なので二倍するとπ/2になるのは、π/4と 5π/4
>cos(π/4) + i sin(π/4) は 1/√2 + i/√2
>cos(5π/4) + i sin(5π/4) は -1/√2 + (-i/√2)
>となり、AQさんの
>±1/√2 ± i/√2(複号同順)
>と同じ結果になります。
この議論を詳述すると、mode 計算をイメージできます。
かけ算は、指数にとっては足し算なので、
円を8等分する8の剰余系の足し算を考えます。
これは45度ずつの対応を考えることと同じ事なのが判ります。
0+0=0, 0+1=0, 0+2=2, 0+3=3, 0+4=4, 0+5=5, 0+6=6, 0+7=7,
1+0=1, 1+1=2, 1+2=3, 1+3=4, 1+4=5, 1+5=6, 1+6=7, 1+7=0,
2+0=2, 2+1=3, 2+2=4, 2+3=5, 2+4=6, 2+5=7, 2+6=0, 2+7=1,
3+0=3, 3+1=4, 3+2=5, 3+3=6, 3+4=7, 3+5=0, 3+6=1, 3+7=2,
4+0=4, 4+1=5, 4+2=6, 4+3=7, 4+4=0, 4+5=1, 4+6=2, 4+7=3,
5+0=5, 5+1=6, 5+2=7, 5+3=0, 5+4=1, 5+5=2, 5+6=3, 5+7=4,
6+0=6, 6+1=7, 6+2=8, 6+3=1, 6+4=2, 6+5=3, 6+6=4, 6+7=5,
7+0=7, 7+1=0, 7+2=1, 7+3=2, 7+4=3, 7+5=4, 7+6=5, 7+7=6,
ここで、同じ数を足して、2(90度)になるのは、1+1=2, 5+5=2,
因みに、-iを得るためには、同じ数を足して、6(270度)になればいいので、3+3=6, 7+7=6
複素平面の単位円を8等分して、
1の8乗根ζ_8を考えます。 これをあらためて、ζとすると、
ζのかけ算は、上の表に従います。
ζ=cos(2π(1/8))+isin(2π(1/8))=cos(π/4)+isin(π/4)=1/√2+i/√2
ζ^5=cos(2π(5/8))+isin(2π(5/8))=cos(5π/4)+isin(5π/4)=-1/√2-i/√2
上の二つは、2乗してiになるもの、別に2乗して-iになるものを考えると
これは、4乗して-1になるもの、つまりは、x^4+1=0を満足していることがわかる。
x^4+1=(x^2+i)(x^2-i)=0
このx^4+1は、実数の範囲でこれ以上因数分解出来ないので、既約多項式である。
8乗根の場合の円周等分多項式のというそうです。
>cos(π/2) + i sin(π/2) = i
>なので二倍するとπ/2になるのは、π/4と 5π/4
>cos(π/4) + i sin(π/4) は 1/√2 + i/√2
>cos(5π/4) + i sin(5π/4) は -1/√2 + (-i/√2)
>となり、AQさんの
>±1/√2 ± i/√2(複号同順)
>と同じ結果になります。
この議論を詳述すると、mode 計算をイメージできます。
かけ算は、指数にとっては足し算なので、
円を8等分する8の剰余系の足し算を考えます。
これは45度ずつの対応を考えることと同じ事なのが判ります。
0+0=0, 0+1=0, 0+2=2, 0+3=3, 0+4=4, 0+5=5, 0+6=6, 0+7=7,
1+0=1, 1+1=2, 1+2=3, 1+3=4, 1+4=5, 1+5=6, 1+6=7, 1+7=0,
2+0=2, 2+1=3, 2+2=4, 2+3=5, 2+4=6, 2+5=7, 2+6=0, 2+7=1,
3+0=3, 3+1=4, 3+2=5, 3+3=6, 3+4=7, 3+5=0, 3+6=1, 3+7=2,
4+0=4, 4+1=5, 4+2=6, 4+3=7, 4+4=0, 4+5=1, 4+6=2, 4+7=3,
5+0=5, 5+1=6, 5+2=7, 5+3=0, 5+4=1, 5+5=2, 5+6=3, 5+7=4,
6+0=6, 6+1=7, 6+2=8, 6+3=1, 6+4=2, 6+5=3, 6+6=4, 6+7=5,
7+0=7, 7+1=0, 7+2=1, 7+3=2, 7+4=3, 7+5=4, 7+6=5, 7+7=6,
ここで、同じ数を足して、2(90度)になるのは、1+1=2, 5+5=2,
因みに、-iを得るためには、同じ数を足して、6(270度)になればいいので、3+3=6, 7+7=6
複素平面の単位円を8等分して、
1の8乗根ζ_8を考えます。 これをあらためて、ζとすると、
ζのかけ算は、上の表に従います。
ζ=cos(2π(1/8))+isin(2π(1/8))=cos(π/4)+isin(π/4)=1/√2+i/√2
ζ^5=cos(2π(5/8))+isin(2π(5/8))=cos(5π/4)+isin(5π/4)=-1/√2-i/√2
上の二つは、2乗してiになるもの、別に2乗して-iになるものを考えると
これは、4乗して-1になるもの、つまりは、x^4+1=0を満足していることがわかる。
x^4+1=(x^2+i)(x^2-i)=0
このx^4+1は、実数の範囲でこれ以上因数分解出来ないので、既約多項式である。
8乗根の場合の円周等分多項式のというそうです。
新参者で申し訳ないです。
とても数式について行けないので、あくまで「私見」とお断りさせて頂きますが「発明」という概念は
その仕組み・働きが明確に理論立てられる物に対してだけ使う方が正しいように考えます。
エジソンが出てきましたので「数学」と離れますが、彼は「発明王」として名高い反面
「エジソン効果」という現象を「発見した」とされています。
これは白熱電球の研究中、熱っせられたフィラメントから他方の離れた「電極」に一方向に
電流が流れるというものを「理屈は判らないがこのような現象が起こった」として発表されました。
今やこの発見が「真空管」「半導体」の本質的な基礎原理の元になっていますが彼は「発明」とは
言いませんでした。
数学でも、自然科学でもこれは半ば「原則」として
仕組みそのものをほぼ全て説明出来る事は 「発明」
そうではなく、何らかの論理的な証明乃至説明が完全ではないことは 「発見」
このような流れではと思われるのですが、如何でしょうか。
それであれば、0 も 虚数も 「発見」ではないかと思うのですが。
とても数式について行けないので、あくまで「私見」とお断りさせて頂きますが「発明」という概念は
その仕組み・働きが明確に理論立てられる物に対してだけ使う方が正しいように考えます。
エジソンが出てきましたので「数学」と離れますが、彼は「発明王」として名高い反面
「エジソン効果」という現象を「発見した」とされています。
これは白熱電球の研究中、熱っせられたフィラメントから他方の離れた「電極」に一方向に
電流が流れるというものを「理屈は判らないがこのような現象が起こった」として発表されました。
今やこの発見が「真空管」「半導体」の本質的な基礎原理の元になっていますが彼は「発明」とは
言いませんでした。
数学でも、自然科学でもこれは半ば「原則」として
仕組みそのものをほぼ全て説明出来る事は 「発明」
そうではなく、何らかの論理的な証明乃至説明が完全ではないことは 「発見」
このような流れではと思われるのですが、如何でしょうか。
それであれば、0 も 虚数も 「発見」ではないかと思うのですが。
みなさま
勉強のために書いているところもあって、混乱をもたらすかもしれませんがご容赦下さいませ。
いま、数論I(加藤和也、黒川重信、斎藤毅著)、初等整数論講義(高木貞治著)、といった本を中心に、代数幾何や数論、ゼータ関数などを理解しようと読んでいます。そうすると、複素数に関する基本的なことの理解が深まるように
感じています。
数には、整数(Z)、有理数(Q)、実数(R)、複素数(C)
とあって、古代ギリシャ数学は、有理数をもとにどう実数を正確に定義するか
悩んだのですが(√2が有理数で表せない)、それは19世紀末になって、Cantorが「収束すべき」数列(Cauchy列)の極限としての、実数の定義を考えて解決に至ったとのことです。それに先だって、Dedekindは「有理整数の集合の切断」としての、実数の定義を得ています。
さて、いま、数論に関係すると思われる、P進数なる違った数の概念を理解しようとしています。これは、1900年頃Henselによって導入された実数の世界を拡げた数になっているそうです。これは、いまでも完全に論理的な説明、証明が成されているわけではないとのことです。
P進数について書いた本の最初に以下の記述がありました。複素数について述べています。件の、x^2-i=0、が複素数の中で閉じていることは真に不思議でこれは、ガウスが何種類も証明を考えた代数学の基本定理というそうです。
P9 (p-adic Numbers, p-adic Analysis, and Zeta-Functions, by Neal Koblitz)
ここで、Rは実数、Cは複素数、p-adic NumbersはP進数、| |_p は、p進絶対値のこと。
Getting back to our historical survey, we've gotten as far as R. Next, returning to the first method - solving equations - mathematicians decided that it would be a good idea to have numbers that could solve equations like x^2+1=0. (This is taking things in logical order; historically speaking, the definition of the complex numbers came before the rigorous definition of the real numbers in terms of Cauchy sequences.) Then an amazing thing happened! As soon as i=√(-1) was introduced and the field of complex numbers of the form a+bi, a,b∈R, was defined, it turned out that:
(1)All polynominal equations with coefficients in C have solutions in C - this is the famous Fundamental Theorem of Algebra (the concise terminology is to say that C is algebraically closed); and
(2) C is already "complete" with respect to the (unique) norm which extends the norm | | on R (this norm is given by |a+bi|=√(a^2+b^2), i.e., any Cauchy sequence {a_j + b_ji} has a limit of the form a+bi (since {a_j}, and {b_j} will each be Cauchy sequences in R, you just let a and b their limits).
So the process stops with C, which is only a "quadratic extention" of R (i.e., obtained by adjoining a solution of the quadratic equation x^2+1=0). C is an algebraically closed field which is complete with respect to the Arichimedean metric.
But alas! Such is not to be the case with | |_p .......
複素数体C の重要な代数的性質は,C が代数的閉体であるということである.すなわち,C の元を係数とする任意の多項式f(x) に対して,代数方程式f(x)=0 は必ずC の中に解を持つ(C. F. Gaussに よる代数学の基本定理), 数学辞典第4版P394
複素数α=a+bi に対し,その絶対値(absolute value modulus)|α|を|a+bi|=√(a^2+b^2)=√αα'で定義する。α,βの距離ρ(α,β) を,ρ(α,β)=|α−β| によって定義すれば,ρ(α,β) は距離関数の公理を満たし,C は距離空間となる.この距離に関し,C は局所コンパクトで完備な距離空間である.数学辞典第4版P394
参考文献 数学辞典第4版P395
複素数の導入の歴史や応用については[2],1次変換については[1],[3].
[1]L. V. Ahlfors, Complex analysis, McGraw-Hill, 1953,(邦訳)複素解析, 現代数学社, 1982;[2]H.-D. Ebbinghaus 他編, Zahlen, Springer, 1983,(邦訳)数, 上・下, シュプリンガー・フェアラーク東京, 1991;
[3]L. R. Ford, Automorphic functions,McGraw-Hill, 1929(Chelsea, 1951).
勉強のために書いているところもあって、混乱をもたらすかもしれませんがご容赦下さいませ。
いま、数論I(加藤和也、黒川重信、斎藤毅著)、初等整数論講義(高木貞治著)、といった本を中心に、代数幾何や数論、ゼータ関数などを理解しようと読んでいます。そうすると、複素数に関する基本的なことの理解が深まるように
感じています。
数には、整数(Z)、有理数(Q)、実数(R)、複素数(C)
とあって、古代ギリシャ数学は、有理数をもとにどう実数を正確に定義するか
悩んだのですが(√2が有理数で表せない)、それは19世紀末になって、Cantorが「収束すべき」数列(Cauchy列)の極限としての、実数の定義を考えて解決に至ったとのことです。それに先だって、Dedekindは「有理整数の集合の切断」としての、実数の定義を得ています。
さて、いま、数論に関係すると思われる、P進数なる違った数の概念を理解しようとしています。これは、1900年頃Henselによって導入された実数の世界を拡げた数になっているそうです。これは、いまでも完全に論理的な説明、証明が成されているわけではないとのことです。
P進数について書いた本の最初に以下の記述がありました。複素数について述べています。件の、x^2-i=0、が複素数の中で閉じていることは真に不思議でこれは、ガウスが何種類も証明を考えた代数学の基本定理というそうです。
P9 (p-adic Numbers, p-adic Analysis, and Zeta-Functions, by Neal Koblitz)
ここで、Rは実数、Cは複素数、p-adic NumbersはP進数、| |_p は、p進絶対値のこと。
Getting back to our historical survey, we've gotten as far as R. Next, returning to the first method - solving equations - mathematicians decided that it would be a good idea to have numbers that could solve equations like x^2+1=0. (This is taking things in logical order; historically speaking, the definition of the complex numbers came before the rigorous definition of the real numbers in terms of Cauchy sequences.) Then an amazing thing happened! As soon as i=√(-1) was introduced and the field of complex numbers of the form a+bi, a,b∈R, was defined, it turned out that:
(1)All polynominal equations with coefficients in C have solutions in C - this is the famous Fundamental Theorem of Algebra (the concise terminology is to say that C is algebraically closed); and
(2) C is already "complete" with respect to the (unique) norm which extends the norm | | on R (this norm is given by |a+bi|=√(a^2+b^2), i.e., any Cauchy sequence {a_j + b_ji} has a limit of the form a+bi (since {a_j}, and {b_j} will each be Cauchy sequences in R, you just let a and b their limits).
So the process stops with C, which is only a "quadratic extention" of R (i.e., obtained by adjoining a solution of the quadratic equation x^2+1=0). C is an algebraically closed field which is complete with respect to the Arichimedean metric.
But alas! Such is not to be the case with | |_p .......
複素数体C の重要な代数的性質は,C が代数的閉体であるということである.すなわち,C の元を係数とする任意の多項式f(x) に対して,代数方程式f(x)=0 は必ずC の中に解を持つ(C. F. Gaussに よる代数学の基本定理), 数学辞典第4版P394
複素数α=a+bi に対し,その絶対値(absolute value modulus)|α|を|a+bi|=√(a^2+b^2)=√αα'で定義する。α,βの距離ρ(α,β) を,ρ(α,β)=|α−β| によって定義すれば,ρ(α,β) は距離関数の公理を満たし,C は距離空間となる.この距離に関し,C は局所コンパクトで完備な距離空間である.数学辞典第4版P394
参考文献 数学辞典第4版P395
複素数の導入の歴史や応用については[2],1次変換については[1],[3].
[1]L. V. Ahlfors, Complex analysis, McGraw-Hill, 1953,(邦訳)複素解析, 現代数学社, 1982;[2]H.-D. Ebbinghaus 他編, Zahlen, Springer, 1983,(邦訳)数, 上・下, シュプリンガー・フェアラーク東京, 1991;
[3]L. R. Ford, Automorphic functions,McGraw-Hill, 1929(Chelsea, 1951).
みなさま
続きです。
また、以下の7行は、数論Iの読書会の投稿からの写しです。
---------------------
奇素数pをとり、ζ=exp{2πi/p},K=Q(ζ)とおくと、
これは円分体と呼ばれる大変興味深い代数体が得られます。
最小多項式は
f(X)=X^{p−1}+X~{p-2}+…+X+1
で、K/QはAbel拡大であり、そのGalois群は
Gal(K/Q)〜(Z/pZ)^× (同型)
となり、分かりやすい面ももっています。
---------------------------
ここで、x^p=1を満足するので、
x^p-1=(x-1){X^{p−1}+X~{p-2}+…+X+1}=0
が成り立って、結局、自明なx=1を除くと、
f(X)=X^{p−1}+X~{p-2}+…+X+1=0
という関係が出てくる。
先の
cos(π/4) + i sin(π/4) は 1/√2 + i/√2
の例は、
素数では無いのですが、P'=8の場合です。
x^8-1=(x-1)(x^7+x^6+x^5+x^4+x^3+x^2+x+1)
=(x-1)(x+1)(x^2+1)(x^4+1)=0
(x-1)(x+1)(x^2+1)=0に関係する
自明なx=1.-1, i,-iを除くと、
x^4+1=0が残ります。
ここで出てくる、4つの数は、8の剰余系で考えると、
{1,3,5,7}に対応するものです。
因みに、
Gaussが、2次方程式を何段か重ねて解くことによって1の17乗根が得られることを「発見」し、これによって、彼は数学者になる決心をしたというのは
有名な話です。
自明な1を除くと16次の方程式が得られて、16=2^4、ですから、
これを8,4,2次式と半分ずつに解体していくことにより解ける。
これは、何回たどっても本当におもしろい解法ですね。
Gal(K/Q)はガロア拡大を表していて、円分体が、ガロア理論の代表的な
例になっていることが理解できます。
例えば、こんな議論が広がっていきます。
以下も読書会からの投稿のものです。
Q(ζ_8)の部分体をすべて挙げよ。それぞれの体において
完全分解する素数はなにか。という
数論Iの演習問題5.1の解答
-------------------------------------------
以下、ζ_8=ζとおく。1の原始8乗根はζ,ζ^3,ζ^5,ζ^7であり、
既約なf(x)=x^4+1∈Q[x]の根である。
σ,τ∈G=Gal(Q(ζ)/Q)をσ(ζ)=ζ^3,τ(ζ)=ζ^5で定義すると、
στ(ζ)=(ζ^5)^3=ζ^15=ζ^7,τσ(ζ)=(ζ^3)^5=ζ^15=ζ^7から、στ=τσ
従って、G=<σ,τ|σ^2=τ^2=1,στ=τσ>はアーベル群であり、部分群列は、
G⊃H={σ,1}⊃{1}
G⊃I={τ,1}⊃{1}
G⊃J={τσ,1}⊃{1}
Q(ζ)のQに対する拡大次数が4であることから、
Q上基底をζ,ζ^2,ζ^3,ζ^4
【G⊃H={σ,1}⊃{1}に対応するQ(ζ)の部分体列】
ζ-ζ^-1は、Hの同型写像により、固定されるから、
Hに対応するQとQ(ζ)の中間体はQ(ζ-ζ^-1)である。
【G⊃I⊃{1}に対応するQ(ζ)の部分体列】
τ(ζ^2)=ζ^10=ζ^2
即ちζ^2は、Iの同型写像により、固定されるから、
Iに対応するQとQ(ζ)の中間体はQ(ζ^2)である。
【G⊃J⊃{1}に対応するQ(ζ)の部分体列】
同様に、中間体Q(ζ+ζ^-1)を得る。
【まとめ】ζ^4=-1からQ(ζ^2)=Q(√-1)
(ζ+ζ^-1)^2+(ζ-ζ^-1)^2=2(ζ^2+ζ^-2)=0,(ζ+ζ^-1)^2-(ζ-ζ^-1)^2=4
から、(ζ+ζ^-1)^2=2,(ζ-ζ^-1)^2=-2を得る。
従って、Q(ζ+ζ^-1)=Q(√2),Q(ζ-ζ^-1)=Q(√-2)であり、
Q(ζ_8)の部分体列は、
Q(ζ_8)⊃Q(√-2)⊃Q,
Q(ζ_8)⊃Q(√-1)⊃Q,
Q(ζ_8)⊃Q(√2)⊃Qの3通りある。
更に、Gは{1,3,5,7},Hは{1,3},Iは{1,5},Jは{1,7}
と同一視出来るので、
Gal(Q(ζ_8)/Q(ζ_8))={1}から、Q(ζ_8)はp≡1 mod 8
Gal(Q(ζ_8)/Q(√-2))=Hから、Q(√-2)はp≡1,3 mod 8
Gal(Q(ζ_8)/Q(√-1))=Iから、Q(√-1)はp≡1,5 mod 8
(p≡1 mod 4でもある。)
Gal(Q(ζ_8)/Q(√2))=Jから、Q(√2)はp≡1,7 mod 8
Gal(Q(ζ_8)/Q)=Gから、Qはp≡1,3,5,7 mod 8従って、全ての素数
を完全分解する。
-----------------------------------------
続きです。
また、以下の7行は、数論Iの読書会の投稿からの写しです。
---------------------
奇素数pをとり、ζ=exp{2πi/p},K=Q(ζ)とおくと、
これは円分体と呼ばれる大変興味深い代数体が得られます。
最小多項式は
f(X)=X^{p−1}+X~{p-2}+…+X+1
で、K/QはAbel拡大であり、そのGalois群は
Gal(K/Q)〜(Z/pZ)^× (同型)
となり、分かりやすい面ももっています。
---------------------------
ここで、x^p=1を満足するので、
x^p-1=(x-1){X^{p−1}+X~{p-2}+…+X+1}=0
が成り立って、結局、自明なx=1を除くと、
f(X)=X^{p−1}+X~{p-2}+…+X+1=0
という関係が出てくる。
先の
cos(π/4) + i sin(π/4) は 1/√2 + i/√2
の例は、
素数では無いのですが、P'=8の場合です。
x^8-1=(x-1)(x^7+x^6+x^5+x^4+x^3+x^2+x+1)
=(x-1)(x+1)(x^2+1)(x^4+1)=0
(x-1)(x+1)(x^2+1)=0に関係する
自明なx=1.-1, i,-iを除くと、
x^4+1=0が残ります。
ここで出てくる、4つの数は、8の剰余系で考えると、
{1,3,5,7}に対応するものです。
因みに、
Gaussが、2次方程式を何段か重ねて解くことによって1の17乗根が得られることを「発見」し、これによって、彼は数学者になる決心をしたというのは
有名な話です。
自明な1を除くと16次の方程式が得られて、16=2^4、ですから、
これを8,4,2次式と半分ずつに解体していくことにより解ける。
これは、何回たどっても本当におもしろい解法ですね。
Gal(K/Q)はガロア拡大を表していて、円分体が、ガロア理論の代表的な
例になっていることが理解できます。
例えば、こんな議論が広がっていきます。
以下も読書会からの投稿のものです。
Q(ζ_8)の部分体をすべて挙げよ。それぞれの体において
完全分解する素数はなにか。という
数論Iの演習問題5.1の解答
-------------------------------------------
以下、ζ_8=ζとおく。1の原始8乗根はζ,ζ^3,ζ^5,ζ^7であり、
既約なf(x)=x^4+1∈Q[x]の根である。
σ,τ∈G=Gal(Q(ζ)/Q)をσ(ζ)=ζ^3,τ(ζ)=ζ^5で定義すると、
στ(ζ)=(ζ^5)^3=ζ^15=ζ^7,τσ(ζ)=(ζ^3)^5=ζ^15=ζ^7から、στ=τσ
従って、G=<σ,τ|σ^2=τ^2=1,στ=τσ>はアーベル群であり、部分群列は、
G⊃H={σ,1}⊃{1}
G⊃I={τ,1}⊃{1}
G⊃J={τσ,1}⊃{1}
Q(ζ)のQに対する拡大次数が4であることから、
Q上基底をζ,ζ^2,ζ^3,ζ^4
【G⊃H={σ,1}⊃{1}に対応するQ(ζ)の部分体列】
ζ-ζ^-1は、Hの同型写像により、固定されるから、
Hに対応するQとQ(ζ)の中間体はQ(ζ-ζ^-1)である。
【G⊃I⊃{1}に対応するQ(ζ)の部分体列】
τ(ζ^2)=ζ^10=ζ^2
即ちζ^2は、Iの同型写像により、固定されるから、
Iに対応するQとQ(ζ)の中間体はQ(ζ^2)である。
【G⊃J⊃{1}に対応するQ(ζ)の部分体列】
同様に、中間体Q(ζ+ζ^-1)を得る。
【まとめ】ζ^4=-1からQ(ζ^2)=Q(√-1)
(ζ+ζ^-1)^2+(ζ-ζ^-1)^2=2(ζ^2+ζ^-2)=0,(ζ+ζ^-1)^2-(ζ-ζ^-1)^2=4
から、(ζ+ζ^-1)^2=2,(ζ-ζ^-1)^2=-2を得る。
従って、Q(ζ+ζ^-1)=Q(√2),Q(ζ-ζ^-1)=Q(√-2)であり、
Q(ζ_8)の部分体列は、
Q(ζ_8)⊃Q(√-2)⊃Q,
Q(ζ_8)⊃Q(√-1)⊃Q,
Q(ζ_8)⊃Q(√2)⊃Qの3通りある。
更に、Gは{1,3,5,7},Hは{1,3},Iは{1,5},Jは{1,7}
と同一視出来るので、
Gal(Q(ζ_8)/Q(ζ_8))={1}から、Q(ζ_8)はp≡1 mod 8
Gal(Q(ζ_8)/Q(√-2))=Hから、Q(√-2)はp≡1,3 mod 8
Gal(Q(ζ_8)/Q(√-1))=Iから、Q(√-1)はp≡1,5 mod 8
(p≡1 mod 4でもある。)
Gal(Q(ζ_8)/Q(√2))=Jから、Q(√2)はp≡1,7 mod 8
Gal(Q(ζ_8)/Q)=Gから、Qはp≡1,3,5,7 mod 8従って、全ての素数
を完全分解する。
-----------------------------------------
今回は、ここまでです。
-------------------------
ζ_8については、
こんなのもありました。数論IのP105演習問題3.3
ζ_8= cos(π/4) + i sin(π/4)=(1+i)/√2,
とし、a=1,3,5,7に対し、
s_a=Σ[n=1,∞]{ζ_8^(an)}/n= -log {1-ζ_8^(a)} と置く。
s_1-s_3-s_5+s_7を計算することにより、
1-1/3-1/5+1/7+1/9-1/11-1/13+1/15
+---(正負の符号は8ごとに繰り返す)
=(1/√2)log(1+√2)
の公式を証明せよ。(Dirichletの公式)
---------
L(1, χ)=Σ[n=1,∞]χ(n)/n
と置きこれをχについてのDirichlet L関数と呼ぶ。
ここでχ(n)はDirichlet指標
χ(1 mod 8)=χ(7 mod 8)=1, χ(3 mod 8)=χ(5 mod 8)=-1
s_1-s_3-s_5+s_7
= -log{1-ζ_8}{1-ζ_8^(7)}/{1-ζ_8^(3)}{1-ζ_8^(5)} ?
ζ_8= (1+i)/√2, ζ_8^(3)=(-1+i)/√2
ζ_8^(5)=(-1-i)/√2, ζ_8^(7)= (1-i)/√2
を?に代入すると
s_1-s_3-s_5+s_7 = 2 log(1+√2) ?
一方:
s_1-s_3-s_5+s_7
={ζ_8-ζ_8^(3)-ζ_8(5)+ζ_8^(7)}Σ[n=1,∞]χ(n)/n ?
ζ_8-ζ_8^(3)-ζ_8(5)+ζ_8^(7)
=(1+i)/√2-(-1+i)/√2-(-1-i)/√2+(1-i)/√2 = 2√2
なので、 ?に代入して、
s_1-s_3-s_5+s_7=2√2*L(1, χ) ?
??より、L(1, χ)=(1/√2)log(1+√2)
-----------------------
長くなりました。
こういったことが、発見といえるのか、発明といえるのか。
知人のひとりは、夏目漱石の夢十夜、運慶の文章を紹介しています。
「能くああ無造作に鑿を使って、思う様な眉や鼻ができるものだな」と自
分はあんまり感心したから独言の様に言った。するとさっきの若い男が、
「なに、あれは眉や鼻を鑿で作るんじゃない。あの通りの眉や鼻が木の中
に埋っているのを、鑿と槌の力で掘り出すまでだ。まるで土の中から石を
掘り出す様なものだから決して間違う筈はない」と云った。
-------------------------
ζ_8については、
こんなのもありました。数論IのP105演習問題3.3
ζ_8= cos(π/4) + i sin(π/4)=(1+i)/√2,
とし、a=1,3,5,7に対し、
s_a=Σ[n=1,∞]{ζ_8^(an)}/n= -log {1-ζ_8^(a)} と置く。
s_1-s_3-s_5+s_7を計算することにより、
1-1/3-1/5+1/7+1/9-1/11-1/13+1/15
+---(正負の符号は8ごとに繰り返す)
=(1/√2)log(1+√2)
の公式を証明せよ。(Dirichletの公式)
---------
L(1, χ)=Σ[n=1,∞]χ(n)/n
と置きこれをχについてのDirichlet L関数と呼ぶ。
ここでχ(n)はDirichlet指標
χ(1 mod 8)=χ(7 mod 8)=1, χ(3 mod 8)=χ(5 mod 8)=-1
s_1-s_3-s_5+s_7
= -log{1-ζ_8}{1-ζ_8^(7)}/{1-ζ_8^(3)}{1-ζ_8^(5)} ?
ζ_8= (1+i)/√2, ζ_8^(3)=(-1+i)/√2
ζ_8^(5)=(-1-i)/√2, ζ_8^(7)= (1-i)/√2
を?に代入すると
s_1-s_3-s_5+s_7 = 2 log(1+√2) ?
一方:
s_1-s_3-s_5+s_7
={ζ_8-ζ_8^(3)-ζ_8(5)+ζ_8^(7)}Σ[n=1,∞]χ(n)/n ?
ζ_8-ζ_8^(3)-ζ_8(5)+ζ_8^(7)
=(1+i)/√2-(-1+i)/√2-(-1-i)/√2+(1-i)/√2 = 2√2
なので、 ?に代入して、
s_1-s_3-s_5+s_7=2√2*L(1, χ) ?
??より、L(1, χ)=(1/√2)log(1+√2)
-----------------------
長くなりました。
こういったことが、発見といえるのか、発明といえるのか。
知人のひとりは、夏目漱石の夢十夜、運慶の文章を紹介しています。
「能くああ無造作に鑿を使って、思う様な眉や鼻ができるものだな」と自
分はあんまり感心したから独言の様に言った。するとさっきの若い男が、
「なに、あれは眉や鼻を鑿で作るんじゃない。あの通りの眉や鼻が木の中
に埋っているのを、鑿と槌の力で掘り出すまでだ。まるで土の中から石を
掘り出す様なものだから決して間違う筈はない」と云った。
waku=wakuさん、Kerberousさん、みなさま
ちょうど、持ってきている
「代数方程式のガロア理論」Jean-Pierre Tignol著
の28ページに、
何よりもまず、方程式を扱うための適当な記号を創出する
必要があった。ことが紹介されています。
16世紀のカルダーノによると、
(5+√(-15))(5-√(-15))
=25-(-15)
=40
は、
5p : Rm :15
5m : Rm :15
--------------
25m: m :15 qd est 40
pはプラス、mはマイナス、Rはルートを表す。
記号の標準化は、発明と云えるかもしれませんね。
おやおや、√(-15)が、と思った次第。
この本の80ページには、ライプニッツが、
x^4+1
=(x^2+√(-1))(x^2-√(-1))
=(x+√√(-1))(x-√√(-1))(x+√-√(-1))=(x-√-√(-1))
に対して、
√√(-1))=(1+√(-1)/√2,
√-√(-1))=(1-√(-1)/√2,
に気づかなかったエピソードが載っています。
ドモアブルの公式ができあがっていく過程を
解説してあって、まことに興味深い。
n乗根をとっていく方向と、累乗する方向が
一致するのがおもしろいですね。
ガロアやアーベルの方程式論が
本の主題ではありますが、そこはおいておいても
その他がなかなか興味を引いて、高校の数学でも
理解しやすく思いました。立ち読みでもしてくださいませ。
注1:
体Q(√(-2))={a+b√(-2);a,b∈Q} (Qは有理数全体)
体Q(ζ_8))={a+b√(ζ_8);a,b∈Q} (Qは有理数全体)
と云った記号です。
また、
体Q(√(-1))={a+bi;a,b∈Q} (Qは有理数全体)
は、複素数に近く感じますが、
複素数は、a,b∈R(実数)でしたね。
注2:
x^4+1は、8の円分多項式で
x^8-1=0を展開すると、
x^8-1=(x-1)(x+1)(x^2+1)(x^4+1)
となることが判ります。
ここで、x=1,-1,i,-iは原始根にならない。
x^4+1=0の解だけ、原始根になる。
例えば、1の8乗根ζについて、そのζ^5のべき乗を考えます。
>cos(5π/4) + i sin(5π/4) は -1/√2 + (-i/√2)
>に相当するものですが、
ζ^5,
(ζ^5)^2=ζ^10=ζ^(8+2)=ζ^2
(ζ^5)^3=ζ^15=ζ^(8+7)=ζ^7
指数を8の剰余系で計算していくと
ζ^5の累乗の指数は、ζ^5:5,2,7,4,1,6,3,8=0 となります。
9乗目ではじめて元に戻る。
原始根の概念が判ったときはうれしかった。
注3:コメント56の
>0+0=0, 0+1=0,..
は
>0+0=0, 0+1=1,...
に訂正します。
ちょうど、持ってきている
「代数方程式のガロア理論」Jean-Pierre Tignol著
の28ページに、
何よりもまず、方程式を扱うための適当な記号を創出する
必要があった。ことが紹介されています。
16世紀のカルダーノによると、
(5+√(-15))(5-√(-15))
=25-(-15)
=40
は、
5p : Rm :15
5m : Rm :15
--------------
25m: m :15 qd est 40
pはプラス、mはマイナス、Rはルートを表す。
記号の標準化は、発明と云えるかもしれませんね。
おやおや、√(-15)が、と思った次第。
この本の80ページには、ライプニッツが、
x^4+1
=(x^2+√(-1))(x^2-√(-1))
=(x+√√(-1))(x-√√(-1))(x+√-√(-1))=(x-√-√(-1))
に対して、
√√(-1))=(1+√(-1)/√2,
√-√(-1))=(1-√(-1)/√2,
に気づかなかったエピソードが載っています。
ドモアブルの公式ができあがっていく過程を
解説してあって、まことに興味深い。
n乗根をとっていく方向と、累乗する方向が
一致するのがおもしろいですね。
ガロアやアーベルの方程式論が
本の主題ではありますが、そこはおいておいても
その他がなかなか興味を引いて、高校の数学でも
理解しやすく思いました。立ち読みでもしてくださいませ。
注1:
体Q(√(-2))={a+b√(-2);a,b∈Q} (Qは有理数全体)
体Q(ζ_8))={a+b√(ζ_8);a,b∈Q} (Qは有理数全体)
と云った記号です。
また、
体Q(√(-1))={a+bi;a,b∈Q} (Qは有理数全体)
は、複素数に近く感じますが、
複素数は、a,b∈R(実数)でしたね。
注2:
x^4+1は、8の円分多項式で
x^8-1=0を展開すると、
x^8-1=(x-1)(x+1)(x^2+1)(x^4+1)
となることが判ります。
ここで、x=1,-1,i,-iは原始根にならない。
x^4+1=0の解だけ、原始根になる。
例えば、1の8乗根ζについて、そのζ^5のべき乗を考えます。
>cos(5π/4) + i sin(5π/4) は -1/√2 + (-i/√2)
>に相当するものですが、
ζ^5,
(ζ^5)^2=ζ^10=ζ^(8+2)=ζ^2
(ζ^5)^3=ζ^15=ζ^(8+7)=ζ^7
指数を8の剰余系で計算していくと
ζ^5の累乗の指数は、ζ^5:5,2,7,4,1,6,3,8=0 となります。
9乗目ではじめて元に戻る。
原始根の概念が判ったときはうれしかった。
注3:コメント56の
>0+0=0, 0+1=0,..
は
>0+0=0, 0+1=1,...
に訂正します。
みなさま
どうも長くなってきましたが、ご容赦下さい。大学教養部の数学は好く判らなかったし、高校や受験の数学でイメージが閉じているのをなんとか拡げていきたいと思って、ついつい、深入りします。次の展開に飛翔しなくてはいけないとも思いますので、すこし、拘泥しすぎたかと反省しています。
さて、表と裏について、展開してみます。
『群の発見』(原田耕一郎著,岩波書店)、ガロアと方程式 草場公邦著、で出会ったのですが、正2面体群というのがあるそうです。
群の発見では、背表紙のある本を正面(左に背表紙)に置いて、(右回りがいいでしょう)裏返す操作?と、(同じ面で)90度回転させる操作?を逆順にやると、背表紙の位置が違ってくることから、これは入れ替えの効かない、(アーベル群でない)操作であることが理解できることが書いてあったように記憶しています。?→?だと背表紙は下に、?→?だと背表紙は上にくるのが判ります。
大学の初年のベクトル解析では、ローテーションを習いますが、どうして、マイナスの符号がついてくるのかはっきりしなかったのですが、位相がちがってくるので、プラス・マイナスで分けるのだろうと最近、理解しました。きっとこの性質は我々の住む3次元空間での特徴のひとつなのでありましょう。現在では、スペースシャトルの姿勢制御のために3次元の回転を表すのに、4元数を使うと効きましたが、これなども同じことがらの延長のように思えます。
以下は、よく読むことのあるる数学コラムからの抜粋です。
代数方程式と群
http://www.geocities.jp/ikuro_kotaro/koramu/281_gal.htm
---------------------
「正2面体群」とは,正n角形をそれ自身に移す回転全体のなす群であって,重心を通る垂直軸を中心としたパイ回転(180度の裏表反転)と対称軸を中心としたn回転から生成される位数2nの群と幾何学的に考えることができます.この正2面体という奇妙な名前は,2枚の正多角形を貼り合わせたものをつぶれた多面体と見なすことから由来しているのですが,
2つの生成元a,bがa^2=b^n=(ab)^2=1という関係を満たす。
D2(位数4の正2面体群)はクラインの4元群と呼ばれるもので,長方形(菱形)の対称性のなす群であり,クラインの4元群のすべての元は2乗すると単位元になることから,自分自身が逆元という特徴をもっている.クラインの4元群をD2と表すのは,それが仮想的な正2角形の対称変換群と見なされるからである.
D2=Z2×Z2
位数4の群は,同型であるものを除いて,巡回群C4と直積Z2×Z2の2つしかない.
-------------------------
さて、件のx^4+1を8の剰余系のかけ算を、考えてみると、これは、
クラインの4元群になっているようです。したがって、これは、2つそして2つと分解できてべき根で解けるといった議論に展開します。円分多項式は解が1の原始根よりなるのでその性質からべき根で解けるとのことです。
ヽ1,3,5,7
1,1,3,5,7
3,3,1,7,5
5,5,7,1,3
7,7,5,3,1
どうも長くなってきましたが、ご容赦下さい。大学教養部の数学は好く判らなかったし、高校や受験の数学でイメージが閉じているのをなんとか拡げていきたいと思って、ついつい、深入りします。次の展開に飛翔しなくてはいけないとも思いますので、すこし、拘泥しすぎたかと反省しています。
さて、表と裏について、展開してみます。
『群の発見』(原田耕一郎著,岩波書店)、ガロアと方程式 草場公邦著、で出会ったのですが、正2面体群というのがあるそうです。
群の発見では、背表紙のある本を正面(左に背表紙)に置いて、(右回りがいいでしょう)裏返す操作?と、(同じ面で)90度回転させる操作?を逆順にやると、背表紙の位置が違ってくることから、これは入れ替えの効かない、(アーベル群でない)操作であることが理解できることが書いてあったように記憶しています。?→?だと背表紙は下に、?→?だと背表紙は上にくるのが判ります。
大学の初年のベクトル解析では、ローテーションを習いますが、どうして、マイナスの符号がついてくるのかはっきりしなかったのですが、位相がちがってくるので、プラス・マイナスで分けるのだろうと最近、理解しました。きっとこの性質は我々の住む3次元空間での特徴のひとつなのでありましょう。現在では、スペースシャトルの姿勢制御のために3次元の回転を表すのに、4元数を使うと効きましたが、これなども同じことがらの延長のように思えます。
以下は、よく読むことのあるる数学コラムからの抜粋です。
代数方程式と群
http://www.geocities.jp/ikuro_kotaro/koramu/281_gal.htm
---------------------
「正2面体群」とは,正n角形をそれ自身に移す回転全体のなす群であって,重心を通る垂直軸を中心としたパイ回転(180度の裏表反転)と対称軸を中心としたn回転から生成される位数2nの群と幾何学的に考えることができます.この正2面体という奇妙な名前は,2枚の正多角形を貼り合わせたものをつぶれた多面体と見なすことから由来しているのですが,
2つの生成元a,bがa^2=b^n=(ab)^2=1という関係を満たす。
D2(位数4の正2面体群)はクラインの4元群と呼ばれるもので,長方形(菱形)の対称性のなす群であり,クラインの4元群のすべての元は2乗すると単位元になることから,自分自身が逆元という特徴をもっている.クラインの4元群をD2と表すのは,それが仮想的な正2角形の対称変換群と見なされるからである.
D2=Z2×Z2
位数4の群は,同型であるものを除いて,巡回群C4と直積Z2×Z2の2つしかない.
-------------------------
さて、件のx^4+1を8の剰余系のかけ算を、考えてみると、これは、
クラインの4元群になっているようです。したがって、これは、2つそして2つと分解できてべき根で解けるといった議論に展開します。円分多項式は解が1の原始根よりなるのでその性質からべき根で解けるとのことです。
ヽ1,3,5,7
1,1,3,5,7
3,3,1,7,5
5,5,7,1,3
7,7,5,3,1
続きです。
f(x)=x^4+1=0 の解のひとつζ_8=α=1/√2+i/√2とすると
f(x)=0の根は
α,1/α=1/√2-i/√2,-α=-1/√2-i/√2,-1/α=-1/√2+i/√2
となっていて、
(x-α)(x+α)(x-1/α)(x+1/α)=0 ●
が成り立っていることが判る。
ここで、1/α=√2/(1+i)の分母分子に1-iをかける。
分母は、(1+i)(1-i)=1-(i)^2=1+1=2となる。
√2/(1+i)*(1-i)/(1-i)=√2(1-i)/2=1/√2-i/√2
といいった関係を使いました。
ガロア群の言葉を使うと、
f(x)=x^4+1=0 の分解体をEとする.G(E/Q)を決定する.
f(x)はQ上既約である.
α=1/√2+i/√2とおくと,f(x)=0の根は
α,1/α=1/√2-i/√2,-α=-1/√2-i/√2,-1/α=-1/√2+i/√2
である.
E=Q(α)で,[E:Q]=4なのでG(E/Q)の位数も4である.
ガロア群は根に推移的に作用するのでG(E/Q)の元で
p:α→-α,q:α→1/α,r:α→-1/α
を満足する操作、p,q,rが有ることが判ります。
単位元eとp,q,rは群Kをなす.(e: α→α)
いわゆるクラインの四元数群である.位数を考えK=G(E/Q)である.
α=ζ_8=ζ≡1 とすると、
1/α=ζ_8^7≡7
-1/α=ζ_8^3≡3
-α=ζ_8^5≡5
実際、e^2: α→α→α,p^2:α→-α→α, q^2:α→1/α→α, r^2:α→-1/α→α
と同じ操作を2回すると元に戻る単位元になります。
●式をもう一度よく観察してみます。
(x-α)(x+α)(x-1/α)(x+1/α)=0
のかけ算の順番をかえて2次式の組み合わせを考えてみると、
(x-α)(x+α)= (x^2-α^2) ?
(x-1/α)(x+1/α)= {x^2-(1/α)^2} ?’
から、(x^2-α^2) {x^2-(1/α)^2}=0
すなわち、(x^2-i)(x^2+i)=0
(x-α)(x-1/α)= (x^2-(α+1/α)x+1) ?
(x+α)(x+1/α)= (x^2-(α+1/α)x+1) ?’
から、(x^2-(α+1/α)x+1) (x^2-(α+1/α)x+1) =0
(x-α)(x+1/α)= (x^2-(α-1/α)x-1) ?
(x+α)(x-1/α)= (x^2+(α-1/α)x-1) ?’
から、(x^2-(α-1/α)x+1) (x^2+(α+1/α)x+1) =0
の3種類の組み合わせとなることが判ります。
ここで、α+1/α=√2, α-1/α=√2*i
これは、8乗根で書き直せば、ζ+ζ^(-1)= √2とζ-ζ^(-1)= √2*i
となっていることが判ります。
また、α^2+(1/α)^2=0も元のα^4+1=0からすぐでます。
なんとも対称性の強い式たちですね。
ζ+ζ^(-1)は実数になって、数論でも円分体の単数を考えるときに
重要だそうです。
-----------------------------
『ガロア理論』J.ロットマン,関口次郎訳,Springer-Verlag 東京発行
練習問題80にf(x)=x^4-10x^2+1=0 の分解体をEとする.G(E/Q)を決定せよ.
との問題があります。
その解答は以下の通りです。これも読書会のネットから拾いました。
上の考察は、これを元にして行ってみました。
----------------------------
f(x)=x^4-10x^2+1=0 の分解体をEとする.G(E/Q)を決定する.
練習問題67と例20から f(x)はQ上既約である.
α=√2+√3とおくと,f(x)=0の根は
α,1/α=-√2+√3,-α=-√2-√3,-1/α=√2-√3
である.
例20からE=Q(α)で,[E:Q]=4なのでG(E/Q)の位数も4である.
練習問題79から,ガロア群は根に推移的に作用するので
G(E/Q)の元で
p:α→-α,q:α→1/α,r:α→-1/α
となるものが存在する.
単位元eとp,q,rは群Kをなす.
いわゆるクラインの四元数群である.
位数を考えK=G(E/Q)である.
丶e,p,q,r
e,e,p,q,r
p,p,e,r,q
q,q,r,e,p
r,r,q,p,e
となっている。
------------------------------------
f(x)=x^4+1=0 の解のひとつζ_8=α=1/√2+i/√2とすると
f(x)=0の根は
α,1/α=1/√2-i/√2,-α=-1/√2-i/√2,-1/α=-1/√2+i/√2
となっていて、
(x-α)(x+α)(x-1/α)(x+1/α)=0 ●
が成り立っていることが判る。
ここで、1/α=√2/(1+i)の分母分子に1-iをかける。
分母は、(1+i)(1-i)=1-(i)^2=1+1=2となる。
√2/(1+i)*(1-i)/(1-i)=√2(1-i)/2=1/√2-i/√2
といいった関係を使いました。
ガロア群の言葉を使うと、
f(x)=x^4+1=0 の分解体をEとする.G(E/Q)を決定する.
f(x)はQ上既約である.
α=1/√2+i/√2とおくと,f(x)=0の根は
α,1/α=1/√2-i/√2,-α=-1/√2-i/√2,-1/α=-1/√2+i/√2
である.
E=Q(α)で,[E:Q]=4なのでG(E/Q)の位数も4である.
ガロア群は根に推移的に作用するのでG(E/Q)の元で
p:α→-α,q:α→1/α,r:α→-1/α
を満足する操作、p,q,rが有ることが判ります。
単位元eとp,q,rは群Kをなす.(e: α→α)
いわゆるクラインの四元数群である.位数を考えK=G(E/Q)である.
α=ζ_8=ζ≡1 とすると、
1/α=ζ_8^7≡7
-1/α=ζ_8^3≡3
-α=ζ_8^5≡5
実際、e^2: α→α→α,p^2:α→-α→α, q^2:α→1/α→α, r^2:α→-1/α→α
と同じ操作を2回すると元に戻る単位元になります。
●式をもう一度よく観察してみます。
(x-α)(x+α)(x-1/α)(x+1/α)=0
のかけ算の順番をかえて2次式の組み合わせを考えてみると、
(x-α)(x+α)= (x^2-α^2) ?
(x-1/α)(x+1/α)= {x^2-(1/α)^2} ?’
から、(x^2-α^2) {x^2-(1/α)^2}=0
すなわち、(x^2-i)(x^2+i)=0
(x-α)(x-1/α)= (x^2-(α+1/α)x+1) ?
(x+α)(x+1/α)= (x^2-(α+1/α)x+1) ?’
から、(x^2-(α+1/α)x+1) (x^2-(α+1/α)x+1) =0
(x-α)(x+1/α)= (x^2-(α-1/α)x-1) ?
(x+α)(x-1/α)= (x^2+(α-1/α)x-1) ?’
から、(x^2-(α-1/α)x+1) (x^2+(α+1/α)x+1) =0
の3種類の組み合わせとなることが判ります。
ここで、α+1/α=√2, α-1/α=√2*i
これは、8乗根で書き直せば、ζ+ζ^(-1)= √2とζ-ζ^(-1)= √2*i
となっていることが判ります。
また、α^2+(1/α)^2=0も元のα^4+1=0からすぐでます。
なんとも対称性の強い式たちですね。
ζ+ζ^(-1)は実数になって、数論でも円分体の単数を考えるときに
重要だそうです。
-----------------------------
『ガロア理論』J.ロットマン,関口次郎訳,Springer-Verlag 東京発行
練習問題80にf(x)=x^4-10x^2+1=0 の分解体をEとする.G(E/Q)を決定せよ.
との問題があります。
その解答は以下の通りです。これも読書会のネットから拾いました。
上の考察は、これを元にして行ってみました。
----------------------------
f(x)=x^4-10x^2+1=0 の分解体をEとする.G(E/Q)を決定する.
練習問題67と例20から f(x)はQ上既約である.
α=√2+√3とおくと,f(x)=0の根は
α,1/α=-√2+√3,-α=-√2-√3,-1/α=√2-√3
である.
例20からE=Q(α)で,[E:Q]=4なのでG(E/Q)の位数も4である.
練習問題79から,ガロア群は根に推移的に作用するので
G(E/Q)の元で
p:α→-α,q:α→1/α,r:α→-1/α
となるものが存在する.
単位元eとp,q,rは群Kをなす.
いわゆるクラインの四元数群である.
位数を考えK=G(E/Q)である.
丶e,p,q,r
e,e,p,q,r
p,p,e,r,q
q,q,r,e,p
r,r,q,p,e
となっている。
------------------------------------
発見か、発明かとの問の趣旨に添えなくなってきたのを勘弁下さいませ。
最近勉強したことを全部書いてみたくなってしまいました。
以下も数論Iのネットの読書会でのコメントです。
ζ+ζ^(-1)について語っています。
-----------------
円分体の単数について、これから様々な深い結果が解説されると思いますが、簡単に分かる性質を少し紹介したいと思います。
奇素数pについて、ζ=e^{2πi/p}、K=Q(ζ)とおくとき、pと互いに素な整数m,nに対して
(1−ζ^m)/(1−ζ^n)
は、Kの単数になります。例4.25から分かる感じですね。理由は考えてみてはいかがでしょうか?
補題4.36についてです。すでに、しっかり理解されていると思いますが、円分体では、Kと、Kの最大実部分体K^+=Q(ζ+ζ^{−1})の関係をいつも意識しておくことが大切だと思っています。そこで、例4.25、例4.26を想定しながら、Kの単数εに対して、ある整数rとK^+の単数ε_1があって、
ε=ζ^r×ε_1
となることが補題4.36より分かります。
例4.25から、
(1−ζ^2)/(1−ζ)=ζ^{1/2}×sin(2π/7)/sin(π/7)
と変形できると思います。したがって、Kの単数はζのあるベキとsinの商に表すことができる。検算をしてみてはいかがでしょうか。わたしが、計算ミスをしていたら申し訳ないが。
----------------------------
以下の式を検算をしてみました。
(1−ζ^2)/(1−ζ)=ζ^{1/2}×sin(2π/7)/sin(π/7) ■
ζ=e^{2πi/7} =cos{2π/7}+i*sin{2π/7} (p=7)
(1−ζ^2)/(1−ζ)
=(1+ζ)
=ζ^{1/2}{ζ^(-1/2)+ζ^(1/2)}
ここで、
ζ^(-1/2)=e^{-πi/7}=cos{π/7}-i*sin{π/7}
ζ^(1/2)=e^{πi/7}=cos{π/7}+i*sin{π/7}、
ζ^(-1/2)+ζ^(1/2)=2cos(π/7)=2cos(π/7){sin(π/7)/sin(π/7)}
=sin(2π/7)/sin(π/7)
ここで、2倍角公式:sin 2α = 2 sin α cos αを使いました。
これで、■式が確認できました。
ζを1のp乗根とすると、
ζ^(-m)+ζ^(m)=2cos(2mπ/p)= 2cos(2mπ/p){sin(2mπ/p)/sin(2mπ/p)}
=sin(4mπ/p)/sin(2mπ/p)
ζを1の8乗根とすると、
ζ^(-m)+ζ^(m)=2cos(2mπ/8)= 2cos(2mπ/8){sin(2mπ/p8/sin(2mπ/8}
=sin(mπ/2)/sin(mπ/4)
m=1とすると、
ζ^(-1)+ζ^(1)=2cos(π/4)=sin(π/2)/sin(π/4)=√2 □
もっとも、複素平面で考えてみれば、
上半面の値と下半面の値を足すわけですから、虚数部分は消えて
実数部分が残りますね。
今回は以上です。どうも失礼しました。
最近勉強したことを全部書いてみたくなってしまいました。
以下も数論Iのネットの読書会でのコメントです。
ζ+ζ^(-1)について語っています。
-----------------
円分体の単数について、これから様々な深い結果が解説されると思いますが、簡単に分かる性質を少し紹介したいと思います。
奇素数pについて、ζ=e^{2πi/p}、K=Q(ζ)とおくとき、pと互いに素な整数m,nに対して
(1−ζ^m)/(1−ζ^n)
は、Kの単数になります。例4.25から分かる感じですね。理由は考えてみてはいかがでしょうか?
補題4.36についてです。すでに、しっかり理解されていると思いますが、円分体では、Kと、Kの最大実部分体K^+=Q(ζ+ζ^{−1})の関係をいつも意識しておくことが大切だと思っています。そこで、例4.25、例4.26を想定しながら、Kの単数εに対して、ある整数rとK^+の単数ε_1があって、
ε=ζ^r×ε_1
となることが補題4.36より分かります。
例4.25から、
(1−ζ^2)/(1−ζ)=ζ^{1/2}×sin(2π/7)/sin(π/7)
と変形できると思います。したがって、Kの単数はζのあるベキとsinの商に表すことができる。検算をしてみてはいかがでしょうか。わたしが、計算ミスをしていたら申し訳ないが。
----------------------------
以下の式を検算をしてみました。
(1−ζ^2)/(1−ζ)=ζ^{1/2}×sin(2π/7)/sin(π/7) ■
ζ=e^{2πi/7} =cos{2π/7}+i*sin{2π/7} (p=7)
(1−ζ^2)/(1−ζ)
=(1+ζ)
=ζ^{1/2}{ζ^(-1/2)+ζ^(1/2)}
ここで、
ζ^(-1/2)=e^{-πi/7}=cos{π/7}-i*sin{π/7}
ζ^(1/2)=e^{πi/7}=cos{π/7}+i*sin{π/7}、
ζ^(-1/2)+ζ^(1/2)=2cos(π/7)=2cos(π/7){sin(π/7)/sin(π/7)}
=sin(2π/7)/sin(π/7)
ここで、2倍角公式:sin 2α = 2 sin α cos αを使いました。
これで、■式が確認できました。
ζを1のp乗根とすると、
ζ^(-m)+ζ^(m)=2cos(2mπ/p)= 2cos(2mπ/p){sin(2mπ/p)/sin(2mπ/p)}
=sin(4mπ/p)/sin(2mπ/p)
ζを1の8乗根とすると、
ζ^(-m)+ζ^(m)=2cos(2mπ/8)= 2cos(2mπ/8){sin(2mπ/p8/sin(2mπ/8}
=sin(mπ/2)/sin(mπ/4)
m=1とすると、
ζ^(-1)+ζ^(1)=2cos(π/4)=sin(π/2)/sin(π/4)=√2 □
もっとも、複素平面で考えてみれば、
上半面の値と下半面の値を足すわけですから、虚数部分は消えて
実数部分が残りますね。
今回は以上です。どうも失礼しました。
若干ホームページもご紹介しておきますね。
http://aozoragakuen.sakura.ne.jp/suuron/node45.html
これは、愛読している青空学園の数論入門のガウス整数についてです。
虚数、複素数のイメージを整理するのに最適だと思います。
いわゆる文系の方々も一読されるときっと理解が深まることでしょう。
http://njet.oops.jp/mt/archives/2004/11/px2y2.html
pを4で割って1余る素数とすると,mod p で i2≡ -1 となる「虚数単位」的な整数 i が存在する。これを使うとx2+y2≡(x+yi)(x-yi)≡0 (mod p)、
すなわちp=x2+y2になる。ちょっと感動しました。
別の角度で、複素数を考えてみると、X^2+1=0の剰余という考えがあるようです。
これは、数学コラムの、因数分解の算法(その3)
http://www.geocities.jp/ikuro_kotaro/koramu/insuubunkai3.htm
にまことに判りやすく紹介してありました。剰余系で考える意味が分かります。
その適用として、フィボナッチ数列と有限体
http://www.geocities.jp/ikuro_kotaro/koramu/suuretsu.htm
には、フィボナッチ数列の周期性の説明がしてあり、そういうものなのかと、少しばかり感動しました。フィボナッチ数列の母関数は、
x^2−x−1=0 とのこと。
これで、この解は、α=(1+√5)/2,β=(1−√5)/2で
有理数に√5を添加した体Q(√5)の素数の分解を考えるとすっきりするようです。これは、件の数論Iの6章の演習問題1にもあります。
テレビで、黄金律やフィボナッチ数列を紹介することがたまにありますが、そのとき、√5という数字すら使うのを避けているような気がして不満です。
黄金比[φ=(√5+1)/2=1.618….]を、8頭身美人云々などとやっていました。世の中の数学アレルギーは強いものがありますね。
数学を語ろう2 代数・数論・数学史篇
三宅 克哉, R.ウィルソン, J.グレイ、シュプリンガー・フェアラーク東京2006年6月9日の6節はR.Cヴォーンの大学教授就任講演でですが、彼の話の出だしがおもしろい。セミナーにいつも出席する者たちよりももっと幅広い聴衆に受け入れられるような話題が選ばれるのが通例でしょう。この意味では純粋数学者は特に不利な立場にあります。その仕事については、他の数学者でさえ理解を行き届かせるのに難儀することがよくあります。しかも高学歴の人たちの多くは数学が全く判らないと誇張して喜ぶ傾向すらあります。
どうも、おじゃましました。
http://aozoragakuen.sakura.ne.jp/suuron/node45.html
これは、愛読している青空学園の数論入門のガウス整数についてです。
虚数、複素数のイメージを整理するのに最適だと思います。
いわゆる文系の方々も一読されるときっと理解が深まることでしょう。
http://njet.oops.jp/mt/archives/2004/11/px2y2.html
pを4で割って1余る素数とすると,mod p で i2≡ -1 となる「虚数単位」的な整数 i が存在する。これを使うとx2+y2≡(x+yi)(x-yi)≡0 (mod p)、
すなわちp=x2+y2になる。ちょっと感動しました。
別の角度で、複素数を考えてみると、X^2+1=0の剰余という考えがあるようです。
これは、数学コラムの、因数分解の算法(その3)
http://www.geocities.jp/ikuro_kotaro/koramu/insuubunkai3.htm
にまことに判りやすく紹介してありました。剰余系で考える意味が分かります。
その適用として、フィボナッチ数列と有限体
http://www.geocities.jp/ikuro_kotaro/koramu/suuretsu.htm
には、フィボナッチ数列の周期性の説明がしてあり、そういうものなのかと、少しばかり感動しました。フィボナッチ数列の母関数は、
x^2−x−1=0 とのこと。
これで、この解は、α=(1+√5)/2,β=(1−√5)/2で
有理数に√5を添加した体Q(√5)の素数の分解を考えるとすっきりするようです。これは、件の数論Iの6章の演習問題1にもあります。
テレビで、黄金律やフィボナッチ数列を紹介することがたまにありますが、そのとき、√5という数字すら使うのを避けているような気がして不満です。
黄金比[φ=(√5+1)/2=1.618….]を、8頭身美人云々などとやっていました。世の中の数学アレルギーは強いものがありますね。
数学を語ろう2 代数・数論・数学史篇
三宅 克哉, R.ウィルソン, J.グレイ、シュプリンガー・フェアラーク東京2006年6月9日の6節はR.Cヴォーンの大学教授就任講演でですが、彼の話の出だしがおもしろい。セミナーにいつも出席する者たちよりももっと幅広い聴衆に受け入れられるような話題が選ばれるのが通例でしょう。この意味では純粋数学者は特に不利な立場にあります。その仕事については、他の数学者でさえ理解を行き届かせるのに難儀することがよくあります。しかも高学歴の人たちの多くは数学が全く判らないと誇張して喜ぶ傾向すらあります。
どうも、おじゃましました。
裏ひろぽんさん
理解が広がっていただいたようで何よりです。そうなんですよね、科学はどんどん進んでいるのに、何年経っても受験時代で留まっているのは何とも残念な事のように思います。
それでは、先の例を使ってもう少し展開してみますね。
件のページには、複素平面が定義してあるので、
それを見ながら、π/4, 3π/4, 5π/4, 7π/4
をもう一度考えてみるのはいかがでしょう。
cos(π/4)+i*sin(π/4)= 1/√2+i/√2=α=ζ_8=ζ
cos(3π/4)+i*sin(3π/4)
=-1/√2+i/√2=[−α~]=−1/α (これは−αの共役複素数)=ζ^3
cos(5π/4)+i*sin(5π/4)=-1/√2-i/√2=−α=ζ^5
cos(7π/4)+i*sin(7π/4)
= 1/√2-i/√2=[α~]=1/α (これはαの共役複素数)=ζ^7
これらは、f(x)=x^4+1=0 の4つの解となっている。
(x-α)(x+α)(x-1/α)(x+1/α)=0
あるいは、
(x-α)(x-(-α))(x-[α~])(x-[-α~])=0
が成り立っていることが判る。
共役複素数をかけあわせると、
α*[α~]={1/√2+i/√2}*{1/√2-i/√2}=(1/√2)^2+(1/√2)^2=1/2+1/2=1
これは、
α*[α~]=α*(1/α)=1 からも判る。
ここで、符号を適宜かえて足し算をしてみる。
ζ-ζ^3-ζ^5+ζ^7=(1/√2)+ (1/√2)+ (1/√2)+ (1/√2)=4 (1/√2)=2√2=√8 ?
となっていることが判る。これをガウス和という。
ここで、ζとζ^7はプラスの符号、ζ^3とζ^5はマイナスの符号、をとった。
一方、符号の組み合わせを少し変えると。
ζ+ζ^3-ζ^5-ζ^7=i√8
と、iの項が残ってくることが判る。
ここの符号の与え方を、(mod Nの)Dirichlet指標:χといい、
これは、χ:(Z/NZ)^(x) → C^(x) と、
Nを自然数とし、環Z/NZの可逆元全体の乗法群(Z/NZ)^(x)から
0でない複素数全体Cの乗法群C^(x)への群準同型を与える。とのことです。
たとえば、?の場合、mod 8 のDirichlet指標となっていて、
χ:(Z/8Z)^(x) = {1 mod 8, 3 mod 8, 5 mod 8, 7 mod 8}→ C^(x)
χ(1 mod 8)=χ(7 mod 8)=1, χ(3 mod 8)=χ(5 mod 8)=-1
また、N(この場合は8)と互いに素でない整数a(この場合は,2,4,6,8等)
については、χ(a)=0と置く。
Σ[a=1,N]χ(a)=0
χ(n)χ(m)=χ(m)χ(n)=χ(nm)
といった性質がある。
このDirichlet指標はリーマンのゼータ関数や、整数論を展開するときによく出てきます。最初は何のことを行っているのかさっぱり判りませんでした。
ウオールストリートでは、リーマンが破綻、世界恐慌が心配されていますが、こちらのリーマンは不滅ですね。
理解が広がっていただいたようで何よりです。そうなんですよね、科学はどんどん進んでいるのに、何年経っても受験時代で留まっているのは何とも残念な事のように思います。
それでは、先の例を使ってもう少し展開してみますね。
件のページには、複素平面が定義してあるので、
それを見ながら、π/4, 3π/4, 5π/4, 7π/4
をもう一度考えてみるのはいかがでしょう。
cos(π/4)+i*sin(π/4)= 1/√2+i/√2=α=ζ_8=ζ
cos(3π/4)+i*sin(3π/4)
=-1/√2+i/√2=[−α~]=−1/α (これは−αの共役複素数)=ζ^3
cos(5π/4)+i*sin(5π/4)=-1/√2-i/√2=−α=ζ^5
cos(7π/4)+i*sin(7π/4)
= 1/√2-i/√2=[α~]=1/α (これはαの共役複素数)=ζ^7
これらは、f(x)=x^4+1=0 の4つの解となっている。
(x-α)(x+α)(x-1/α)(x+1/α)=0
あるいは、
(x-α)(x-(-α))(x-[α~])(x-[-α~])=0
が成り立っていることが判る。
共役複素数をかけあわせると、
α*[α~]={1/√2+i/√2}*{1/√2-i/√2}=(1/√2)^2+(1/√2)^2=1/2+1/2=1
これは、
α*[α~]=α*(1/α)=1 からも判る。
ここで、符号を適宜かえて足し算をしてみる。
ζ-ζ^3-ζ^5+ζ^7=(1/√2)+ (1/√2)+ (1/√2)+ (1/√2)=4 (1/√2)=2√2=√8 ?
となっていることが判る。これをガウス和という。
ここで、ζとζ^7はプラスの符号、ζ^3とζ^5はマイナスの符号、をとった。
一方、符号の組み合わせを少し変えると。
ζ+ζ^3-ζ^5-ζ^7=i√8
と、iの項が残ってくることが判る。
ここの符号の与え方を、(mod Nの)Dirichlet指標:χといい、
これは、χ:(Z/NZ)^(x) → C^(x) と、
Nを自然数とし、環Z/NZの可逆元全体の乗法群(Z/NZ)^(x)から
0でない複素数全体Cの乗法群C^(x)への群準同型を与える。とのことです。
たとえば、?の場合、mod 8 のDirichlet指標となっていて、
χ:(Z/8Z)^(x) = {1 mod 8, 3 mod 8, 5 mod 8, 7 mod 8}→ C^(x)
χ(1 mod 8)=χ(7 mod 8)=1, χ(3 mod 8)=χ(5 mod 8)=-1
また、N(この場合は8)と互いに素でない整数a(この場合は,2,4,6,8等)
については、χ(a)=0と置く。
Σ[a=1,N]χ(a)=0
χ(n)χ(m)=χ(m)χ(n)=χ(nm)
といった性質がある。
このDirichlet指標はリーマンのゼータ関数や、整数論を展開するときによく出てきます。最初は何のことを行っているのかさっぱり判りませんでした。
ウオールストリートでは、リーマンが破綻、世界恐慌が心配されていますが、こちらのリーマンは不滅ですね。
裏ひろぽんさん、みなさま
下記のページは、円周等分多項式をネットで引いてみて偶然見つけたのですが、
ガウスの全集まで遡って、素人にもまことに判りやすくまとめられていて
感銘しています。以下はガウス(20)ですが、1から121まであって、ガウスの数論の研究の全体が判ります。徐々に世界を深められる参考になれば、幸いです。すごい方がおられるものです。
http://reuler.blog108.fc2.com/category3-10.html
因みに件の 1/√2+i/√2は、√2倍すれば、1+i
したがって、
1+i, -1+i, -1-i, 1-i
の四つの解の関係を考察していたとも読めなくもないと気づきました。
この四つは、1,-1,i,-iをかけるとそれぞれ、4つなのかで閉じた動きを
するのが判ります。
2の分解は、2=(-i)(1+i)^2, i(-1+i)^2, (-i)(-1-i)^2, (i)(1-i)^2
などと表されることも判ります。
どうも、1+i, -1+i, -1-i, 1-i は素数に相当するもののようですね。
下記のページは、円周等分多項式をネットで引いてみて偶然見つけたのですが、
ガウスの全集まで遡って、素人にもまことに判りやすくまとめられていて
感銘しています。以下はガウス(20)ですが、1から121まであって、ガウスの数論の研究の全体が判ります。徐々に世界を深められる参考になれば、幸いです。すごい方がおられるものです。
http://reuler.blog108.fc2.com/category3-10.html
因みに件の 1/√2+i/√2は、√2倍すれば、1+i
したがって、
1+i, -1+i, -1-i, 1-i
の四つの解の関係を考察していたとも読めなくもないと気づきました。
この四つは、1,-1,i,-iをかけるとそれぞれ、4つなのかで閉じた動きを
するのが判ります。
2の分解は、2=(-i)(1+i)^2, i(-1+i)^2, (-i)(-1-i)^2, (i)(1-i)^2
などと表されることも判ります。
どうも、1+i, -1+i, -1-i, 1-i は素数に相当するもののようですね。
発明か、発見か、ということですが、発明だと思います。
虚数単位 i が i^2 = -1 を満たす数であることは、そういう仮定を置いたことに他なりません。
すなわち、そのような仮定を「発明」したことになるわけです。
それだけなら非常に退屈な話です。
ただし、発明した体系について、何かを「発見する」ということは頻繁に起こります。
つまり、ある仮定を置いた世界で、思っても見なかったことが起こることが
論理的にいえてしまう、といったことが起こります。
たとえば、iの規則を言い換えてゆくと、自動的にド・モアブルの公式が成り立ってしまったりします。
まったく驚くべきことです。これを知ることは、「発見」にほかなりません。
だから、そもそもひるがえって、仮定を置くという「発明」が有用なのです。
仮に何かを発明したとしても、そこから何も広がっていかなければ、退屈ですよね?
例えば、私が三乗すると-1になる数jを提唱したとしましょう
(こう改めて言うと、これが発明だと分かっていただけると思います)。
そこから現存の複素数のような美しい世界が広がるものでしょうか?
何が「発見」できるでしょうか?
まとめると、
「虚数という発明を行った結果、そのような数を認めた途端、膨大な量の言い換えが発見された」
というところでしょう。
虚数単位 i が i^2 = -1 を満たす数であることは、そういう仮定を置いたことに他なりません。
すなわち、そのような仮定を「発明」したことになるわけです。
それだけなら非常に退屈な話です。
ただし、発明した体系について、何かを「発見する」ということは頻繁に起こります。
つまり、ある仮定を置いた世界で、思っても見なかったことが起こることが
論理的にいえてしまう、といったことが起こります。
たとえば、iの規則を言い換えてゆくと、自動的にド・モアブルの公式が成り立ってしまったりします。
まったく驚くべきことです。これを知ることは、「発見」にほかなりません。
だから、そもそもひるがえって、仮定を置くという「発明」が有用なのです。
仮に何かを発明したとしても、そこから何も広がっていかなければ、退屈ですよね?
例えば、私が三乗すると-1になる数jを提唱したとしましょう
(こう改めて言うと、これが発明だと分かっていただけると思います)。
そこから現存の複素数のような美しい世界が広がるものでしょうか?
何が「発見」できるでしょうか?
まとめると、
「虚数という発明を行った結果、そのような数を認めた途端、膨大な量の言い換えが発見された」
というところでしょう。
> santeさん
笑っちゃいます。
「仮定を発明」
とゆっとりますが、
その仮定で証明される法則は元々あるものではないんですか?
その仮定を証明するのも過去にある事実でしか証明出来ないとおもいますが?
第一、最初に述べてる内容が、
iって概念があるならば、
虚数の法則が証明できます。
って言ってんだから、
元々iがあるって言ってる様なもんじゃん?
それでも発明っていえんの?
三乗を‐1と置く。
それが自然法則に置いて新しい概念なら発明としましょう。
んじゃ其を証明してよ?
その上で発明と発見の違いをいわにゃ。
其が証明出来ない以上、発明でも発明でも無い。
ごっちゃにしないでくださらない?(笑)
纏めると以下も、
「虚数という発見の結果、その様な数を認めた途端、膨大な量の法則が発見された」
でも成り立つとおもうが?
ま、
卑怯な事を言ったら、波の物理式を虚数の概念なしに証明してみろよ。
ってことになります。
波って虚数発見する前からあるからね。
反論宜しく!
笑っちゃいます。
「仮定を発明」
とゆっとりますが、
その仮定で証明される法則は元々あるものではないんですか?
その仮定を証明するのも過去にある事実でしか証明出来ないとおもいますが?
第一、最初に述べてる内容が、
iって概念があるならば、
虚数の法則が証明できます。
って言ってんだから、
元々iがあるって言ってる様なもんじゃん?
それでも発明っていえんの?
三乗を‐1と置く。
それが自然法則に置いて新しい概念なら発明としましょう。
んじゃ其を証明してよ?
その上で発明と発見の違いをいわにゃ。
其が証明出来ない以上、発明でも発明でも無い。
ごっちゃにしないでくださらない?(笑)
纏めると以下も、
「虚数という発見の結果、その様な数を認めた途端、膨大な量の法則が発見された」
でも成り立つとおもうが?
ま、
卑怯な事を言ったら、波の物理式を虚数の概念なしに証明してみろよ。
ってことになります。
波って虚数発見する前からあるからね。
反論宜しく!
既にどなたかが触れられているかも知れませんが……
16世紀の数学者カルダーノによって次の式からの解で虚数が出てくることが確認されています。
x^3=15x+4
これを(a−b)^3=(a^3−b^3)−3ab(a−b)という式に当てはめて展開すると次の式となる。(x=(a−b)として展開する)
x^3=(a−b)^3
15x=−3ab(a−b) → 15=−3ab → ab=−5
4=(a^3−b^3)
b=−a/5を代入して展開。
(a^3)^2−4a^3+125=0
これを2次方程式の解を導く公式に当てはめて計算すると次の結果を得る。
a^3=2±√(−121)
ということで、グラフに書く事ができる2つの線(15x+4とx^3)から虚数が出現する。
つまり、初等数学のグラフの交点を求める場合でも虚数は出現します。
以上、『物理と数学の不思議な関係』マルコム・E・ラインズ著 青木薫 訳 早川書房からの抜粋
結論としては、やはり『発明』ではなく『発見』でしょうね。
16世紀の数学者カルダーノによって次の式からの解で虚数が出てくることが確認されています。
x^3=15x+4
これを(a−b)^3=(a^3−b^3)−3ab(a−b)という式に当てはめて展開すると次の式となる。(x=(a−b)として展開する)
x^3=(a−b)^3
15x=−3ab(a−b) → 15=−3ab → ab=−5
4=(a^3−b^3)
b=−a/5を代入して展開。
(a^3)^2−4a^3+125=0
これを2次方程式の解を導く公式に当てはめて計算すると次の結果を得る。
a^3=2±√(−121)
ということで、グラフに書く事ができる2つの線(15x+4とx^3)から虚数が出現する。
つまり、初等数学のグラフの交点を求める場合でも虚数は出現します。
以上、『物理と数学の不思議な関係』マルコム・E・ラインズ著 青木薫 訳 早川書房からの抜粋
結論としては、やはり『発明』ではなく『発見』でしょうね。
みなさま
飯高茂さんの「数学のかんどころ、群論」同、環論、同体論を
読んで判然としなかったことがふつふつと判ってきた気がしたので、
書きこんでみます。
有理数環Q、実数体R、複素数体C
は、大学の教養課程レベルの
数学の本を読み始めると、最初に書いてあることがしばしばあります。
数学科を出た大学の友人が、群・環・体で代数が嫌になったと
言っていたことを思い出します。
http://www.f-denshi.com/000TokiwaJPN/01daisu/210rng.html
この実数や、複素数が体になるところは、逆数が存在するところが肝のようです。
また、モード計算のように、x^2+1=0 (x=i)をモード(イデアル)とみると、
多項式は、すべて、一次式にできます。つまり、2次以上は、x^2+1=0を使ってどんどん消していくことができる。つまりは、モード計算のように剰余だけを考えればよい。
剰余環や多項式環ということばを知りました。
>実数体R 上の1変数の多項式環R[x] において,多項式 x^2+1 によって生成された
>イデアル (X^2+1)による剰余環R[x]/(x^2+1) と体R(i) は環として同型であることを>示せ。(某大学の代数の試験問題)
体R(i)は、実数にiを加えて拡大した拡大体で、実は複素数体C
http://ufcpp.net/study/set/complex.html
また、複素数を構成していくひとつの試みが、「ガロア理論(上) デイビッド・A・コックス著」のP62あたりに紹介してあってとても感心しました。立ち読み、お勧めです。
(ax+b)(cx+d) ・・・ (1)
=acx^2+(ad+bc)x+bd
=acx^2+ac-ac+(ad+bc)x+bd
=ac(x^2+1)+(ad+bc)x+(bd-ac)
この式を x2+1 で割ると、余りは、 (ad+bc)x+(bd-ac)
一方、(1)の x に i を代入すると、
ac(i)2+(ad+bc)x+bd=(ad+bc)x+(bd-ac)
<x2+1>がモード計算のモードのようになっていることがわかります。これがイデアルらしい。もとの式にac-ac=0を加えるところは、技巧的ですね。
このあたりを、感得することが、大学数学の突破口のようです。
受験数学に立ち止まって展望が開けない、わたしも含めて大多数の科学の入口に立ち止まっている多くの人にとって、ひとつの目標になると思いました。
「代数に惹かれた数学者たち」では、女性数学者のネーターさんの学位論文のことが分かりやすく書かれていたように記憶しています。とにかく、計算ソフトがない時代に、緻密な計算を何万と積み上げて、具体論を徹底的にやったあと、代数の抽象化に取り組んだ人のようです。匠の努力を感じます。
そういった、多くの方の努力と、多数の論文が、新しい概念を試行錯誤を繰り返しながら、作り続けるのでありましょう。新概念もなにか、ひっかかることがなければ、それを考えもしないといったことがありましょうから、もともとあるものの発見の側面がつよい場合もありましょう。
飯高茂さんの「数学のかんどころ、群論」同、環論、同体論を
読んで判然としなかったことがふつふつと判ってきた気がしたので、
書きこんでみます。
有理数環Q、実数体R、複素数体C
は、大学の教養課程レベルの
数学の本を読み始めると、最初に書いてあることがしばしばあります。
数学科を出た大学の友人が、群・環・体で代数が嫌になったと
言っていたことを思い出します。
http://www.f-denshi.com/000TokiwaJPN/01daisu/210rng.html
この実数や、複素数が体になるところは、逆数が存在するところが肝のようです。
また、モード計算のように、x^2+1=0 (x=i)をモード(イデアル)とみると、
多項式は、すべて、一次式にできます。つまり、2次以上は、x^2+1=0を使ってどんどん消していくことができる。つまりは、モード計算のように剰余だけを考えればよい。
剰余環や多項式環ということばを知りました。
>実数体R 上の1変数の多項式環R[x] において,多項式 x^2+1 によって生成された
>イデアル (X^2+1)による剰余環R[x]/(x^2+1) と体R(i) は環として同型であることを>示せ。(某大学の代数の試験問題)
体R(i)は、実数にiを加えて拡大した拡大体で、実は複素数体C
http://ufcpp.net/study/set/complex.html
また、複素数を構成していくひとつの試みが、「ガロア理論(上) デイビッド・A・コックス著」のP62あたりに紹介してあってとても感心しました。立ち読み、お勧めです。
(ax+b)(cx+d) ・・・ (1)
=acx^2+(ad+bc)x+bd
=acx^2+ac-ac+(ad+bc)x+bd
=ac(x^2+1)+(ad+bc)x+(bd-ac)
この式を x2+1 で割ると、余りは、 (ad+bc)x+(bd-ac)
一方、(1)の x に i を代入すると、
ac(i)2+(ad+bc)x+bd=(ad+bc)x+(bd-ac)
<x2+1>がモード計算のモードのようになっていることがわかります。これがイデアルらしい。もとの式にac-ac=0を加えるところは、技巧的ですね。
このあたりを、感得することが、大学数学の突破口のようです。
受験数学に立ち止まって展望が開けない、わたしも含めて大多数の科学の入口に立ち止まっている多くの人にとって、ひとつの目標になると思いました。
「代数に惹かれた数学者たち」では、女性数学者のネーターさんの学位論文のことが分かりやすく書かれていたように記憶しています。とにかく、計算ソフトがない時代に、緻密な計算を何万と積み上げて、具体論を徹底的にやったあと、代数の抽象化に取り組んだ人のようです。匠の努力を感じます。
そういった、多くの方の努力と、多数の論文が、新しい概念を試行錯誤を繰り返しながら、作り続けるのでありましょう。新概念もなにか、ひっかかることがなければ、それを考えもしないといったことがありましょうから、もともとあるものの発見の側面がつよい場合もありましょう。
著名な数学者の文章に惹かれましたので、ご紹介です。
「鳥のように、志村五郎著、筑摩書房、2010」より、メモです。
P132、数学者の仕事
「あまりはっきりとは言い表されない混沌の中から秩序をさがし出し、必要とあれば新しい概念を導入して理論を構成し、新しい原理または事実を定理として示す。」
「「さがし出し」は、「つくり出し」と言ってもよい。出来てしまえば、あたかもそれが隠されていたものを発見したように自然に見えるのであるが。」
「多くの数学者の心を惹きつけているのは、この未知の世界へのあこがれと挑戦、つぎにどうなっていくかわからないというスリルにみちた日々の体験、そして徐々に姿を現してくる秩序の美しさにある。」
「失敗して自信を失わなかった第一級の数学者などというものは非常に稀であろう」
「勝事は空しく(ただ)自ら知る (王維)」
「勤勉とは、実務的かつ散文的な言葉である。」むしろ、「気分をのびやかに持つ必要がある。」
メモ:後世畏るべし。
MIXIの参加者は若い方も多くおられると思います。
畏るべし。で、発展くださいませ。
「鳥のように、志村五郎著、筑摩書房、2010」より、メモです。
P132、数学者の仕事
「あまりはっきりとは言い表されない混沌の中から秩序をさがし出し、必要とあれば新しい概念を導入して理論を構成し、新しい原理または事実を定理として示す。」
「「さがし出し」は、「つくり出し」と言ってもよい。出来てしまえば、あたかもそれが隠されていたものを発見したように自然に見えるのであるが。」
「多くの数学者の心を惹きつけているのは、この未知の世界へのあこがれと挑戦、つぎにどうなっていくかわからないというスリルにみちた日々の体験、そして徐々に姿を現してくる秩序の美しさにある。」
「失敗して自信を失わなかった第一級の数学者などというものは非常に稀であろう」
「勝事は空しく(ただ)自ら知る (王維)」
「勤勉とは、実務的かつ散文的な言葉である。」むしろ、「気分をのびやかに持つ必要がある。」
メモ:後世畏るべし。
MIXIの参加者は若い方も多くおられると思います。
畏るべし。で、発展くださいませ。
- mixiユーザー
- ログインしてコメントしよう!
|
|
|
|
虚数 更新情報
-
最新のイベント
-
まだ何もありません
-
-
最新のアンケート
-
まだ何もありません
-
虚数のメンバーはこんなコミュニティにも参加しています
人気コミュニティランキング
- 1位
- mixi バスケ部
- 37862人
- 2位
- お洒落な女の子が好き
- 90060人
- 3位
- 写真を撮るのが好き
- 208308人