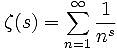ゼータ関数 - Zeta(ζ) Function

詳細 2023年1月21日 19:53更新

ゼータ関数
（ζ関数，Zeta Function，ζ Function）

ζ(s) = Σ[n=1, ∞] 1/(n^s)


ゼータ関数とは，オイラーによって盛んに研究され，リーマンによって名付けられた数学上の概念で，数論の分野に於いて特に重要な関数の一つであり，今も盛んに研究が行われている．

s=1の時のゼータ関数は，調和数列の和の形を取り，収束せずに発散する．
正の偶数のゼータの値はオイラーによって得られた．
ζ(2)=π^2/6，ζ(4)=π^4/90，ζ(6)=π^6/945，ζ(8)=π^8/9450，・・・

然し，奇数のゼータの値は現在に於いても分かっておらず，未解決問題として残っている．
また，負の整数のゼータの値は，オイラーのその研ぎ澄まされた洞察力により，非常に興味深い値を持つ事が知られている．
ζ(0)=-1/2，ζ(-1)=-1/12，ζ(-2)=0，ζ(-3)=1/120，ζ(-4)=0，ζ(-5)=-1/252，・・・

因みに，負の偶数でのゼータの値は全て0になる．これを，ゼータの自明な零点と呼ぶ．
更に，ゼータ関数は，「オイラー積」と同等である事も分かっている．
ζ(s) = Π[p] 1/(1-p^(-s))


数学史上，最大の難問であると言われている「リーマン予想」も，このゼータ関数が非常に密接に関連しており，それは，

「自明でないゼータの零点は，実部が全て1/2である」

という仮説で，リーマンによって問題が提唱されてから現在に至るまで，150年以上経っているにも関わらず未解決のままである．
2000年には，クレイ数学研究所により，この問題の解答に100万ドルの懸賞金が掛けられた事も，有名である．



[説明文更新 ： 2010年8月18日（水）]

• タイムライン
• トピック別

もっと見る