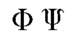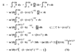場の量子論コミュのポアンカレ群について

場の量子論の初心者です。

培風館　新物理学シリーズ１９
場の量子論　中西襄（ナカニシノボル）著

を読んでいます。
この中で「Poincare群の表現」という項を読んでの疑問です。
ここに書いてあることの要点をざっくり示します。

?Poincare群は平行移動の全体という可換群を含む。

?平行移動のジェネレータＰ^μの固有値p^μに属する固有状態|p>の平行移動は以下になる。
　　exp(-ip_μa_μ)|p>

?Poincare群の既約表現を作ろうとすれば、平行移動の表現exp(-ip_μa_μ)を壊すようなローレンツ変換は許されない。

?よって、Poincare群のlittle groupは以下のように分類される。
　(1)ip_μ が時間的(p^2>0)のとき　　　　　Ｏ(3)
　(2)ip_μ が光錐的(p^2=0，p_0≠0)のとき　Ｅ(2)
　(3)ip_μ が空間的(p^2<0)のとき　　　　　Ｏ(2,1)
　(4)ip_μ=0 のとき　　　　　　　　　　　Ｏ(3,1)

さて、ここで私の疑問ですが、このように分類する意味が解りません。
全ての粒子は時間的あるいは光錐的な運動しかできませんよね？
そうすると、上の(1)と(2)のみとなり、結局粒子に対してはＯ(3)とＥ(2)しか許されないということになるのでしょうか？
頓珍漢な質問だと思いますが、何を解っていないのかが解ってないのだと思います。

コメント(8)

最初
全て
最新の40件

[1] mixiユーザー 12月07日 21:13

Poincare群のlittle groupの意味も知りたいところですが、もう一つ質問があります。

中西襄著「場の量子論」の中では、上記のPoincare群のlittle groupの簡単な説明の後、それがどこにも応用されていないように見受けられます。
Poincare群のlittle groupはいったい何の役に立つのでしょうか？

[2] mixiユーザー 12月09日 02:30

もっと詳しい方が書き込んだ方がいいとも思うのですが、
こういう掲示板は、いろいろ書いた方がいいとも思うので
私なりの意見を書いておきます。間違うかもしれないので
間違っているところは、遠慮なくどなたか訂正してください。

一つ目の質問
「全ての粒子は時間的あるいは光錐的な運動しかできませんよね？
　そうすると、上の(1)と(2)のみとなり、結局粒子に対してはＯ(3)とＥ(2)しか　許されないということになるのでしょうか？」

本には、（３）は許されないが
（４）は粒子も何もない状態、真空に対応すると
書いてあります。真空は重要な概念ですので
（１）、（２）、（４）が許されるという本のとおりでガロアさん
的に問題ないかと思います。
ガロアさんは、粒子が存在するという前提を立ててしまっただけで
考え方もかなり本のとおりのようにお見受けしました。

二つ目の質問
「Poincare群のlittle groupはいったい何の役に立つのでしょうか？」

既約表現という言葉をキーワードに捜すとたくさん例がありそうです。
その中で一番いい例を出すには
私よりもっと詳しい人がいいのですが、とりあえず私のトピックにも
関係しているということで、スピンの分類はどうでしょう？

ｍｉｔさんお勧めの
「ポアンカレ群と波動方程式」大貫義郎　岩波書店
を読んでみるのもいいかもしれません。

[3] mixiユーザー 12月09日 20:26

一応質問１に対して答えた内容は、
ガロアさん引用の本の、Ｐ．５７　３行目です。

ちなみに、「ポアンカレ群と波動方程式」大貫義郎　岩波書店
を読んでいると、この場合を真空としていいのかは
よく考えてみないとと思っています。

[4] mixiユーザー 12月09日 23:11

名犬パピーさん

回答感謝いたします。
しかし残念ながら、本に書いてあることだけが解っても、私としては納得できていないのです。
ｐの値によって変換の種類が制限されることの物理的な意味がさっぱり解らないのです。
たとえば、質量を持つ１つの粒子がある場合、回転変換しか許されないということですよねえ？
しかし、互いに相対速度を持つ２つの慣性系から、この１つの粒子を記述する場合、これらの慣性系の間ではローレンツ変換をすることになりますよね。これが許されないということが私には納得できず、一体どういうことなのだろう？と思うわけです。

[5] mixiユーザー 12月10日 20:19

うーん、
本に書いてあることだけが解ってもだめだとおっしゃられるのは
よくわかるのですが、本が言いたいことを理解するのに
何度もよく読むのは重要だと私はいつも思っています。
そういう癖をつけると、本を理解する力が高くなり
実力が上がるというわけです。

私が思うに
質量を持つ１つの粒子がある場合、
回転変換しか許されないとか
ローレンツ変換をしてはいけないということを言っているわけでは
ないと思いました。

間違っているかもしれませんが、ここでは
ポアンカレ群の既約表現を求めているだけのような気がします。

それがどうなるのといえば、例えば、
(1)ip_μ が時間的(p^2>0)のとき　　　　　Ｏ(3) の場合

質量を持つ粒子の運動量の固有値を確定した場合、
全角運動量はともに確定できますみたいなことを言っていて
別にローレンツ変換しちゃだめよとは言ってないと思いました。

[6] mixiユーザー 12月10日 21:30

名犬パピーさん
コメント有難うございます。

> 何度もよく読むのは重要だと私はいつも思っています。

それは勿論です。しかし、この記述に関しては何度読んでも確認のできない憶測しかできないのです。
これは群論に関する知識が乏しいことも要因だとは思います。

> ポアンカレ群の既約表現を求めているだけのような気がします。

私もそうかもしれないと思っていました。しかしそれもまた憶測です。

> 質量を持つ粒子の運動量の固有値を確定した場合、
> 全角運動量はともに確定できますみたいなことを言っていて

このへんがさすが私よりも先行した知識をお持ちなところだと思いました。
群の既約表現とはそのような使われ方をするものなのですか？

ともかくも、未だポアンカレ群の小群の応用事例を発見することができず、本当のところは闇の中です。

[7] mixiユーザー 12月11日 00:49

ポアンカレ群の小群の応用事例を発見したいのであれば、繰り返しかも
しれませんが、ｍｉｔさんお勧めの「ポアンカレ群と波動方程式」大貫義郎　
岩波書店を読んでみるのもいいかもしれません。

しかし、
「群の既約表現とはそのような使われ方をするものなのですか？」
ガロアさんの最大の関心事は、もしかしたらこれなのかもしれません。
これを仮定して下記を書きます。

既約表現の使われ方は、ガロアさんご指摘のものだけではない気がしますので、
「はい」と答えてしまうとガロアさんにとってもったいない気がしますので
下記のようなコメントをしてみます。多分、もっといろいろ知っている
方がいると思いますので、後はその方のコメントを待ちましょう。

あるｎ次元ベクトル空間Ｖに作用させると、空間Ｖ内にあるｎ次元ベクトルに
移す準同型写像ρで表現された群Ｇを考え、このρを
行列式が０でないｎ×ｎ行列Ａで表すことができたときに、

この群Ｇの既約表現を求めるということは、もうこれ以上簡単な
ブロック化された行列がないブロック行列Ａを求めることを
意味すると思います。なぜなら、不変な部分空間が自分自身と｛０｝しか
ないのが既約なので。

（ブロック行列については、図を描けば一発なのですが、言葉で
　述べるのはなかなか難しいです。対角化がいい例で、この場合１×１が
　対角部に並んでいますが、途中２×２や３×３が対角部にあっても
　いいような形です。それ以外の項は全て０です）

これはすでにガロアさんもご承知のことかもしれませんが
仮に上記群Ｇが量子論における、ある物理量を表す演算子であって
その既約表現を求めてみたときに完全に対角化できたとしましょう。
これは量子論的には系のそれらの状態について、
そのとりうる物理量の値が確定していることを
意味するでしょう。

途中２×２のブロック部が入っていると、
この部分については、その部分の物理量が確定していない
こともわかるでしょう。

例えば、群Ｇが相互作用を表す演算子の場合で
既約表現を求めると、その相互作用により遷移する状態間は
どれとどれだろう、うつらないのはどれとどれだろうなどと
いうことを求めることができる場合もあるでしょう。

他にもいろいろありそうです。

[8] mixiユーザー 12月29日 22:40

名犬パピーさん

「ポアンカレ群と波動方程式」は近所の図書館にて入手できることがわかりました。
その他、ご教授ありがとうございました。

ログインすると、みんなのコメントがもっと見れるよ