直交表 というものがあります。 詳しい方はぜひコメントください。
これが、ラテン方陣に基づくもので、魔方陣に関係ありという話です。
(少しは、魔方陣にも、実用的な意味があることを示したいといったところです。)
直交表は、実験計画法や品質工学に、でてくる内容で複数因子間の組合せに漏れが無いようにしながら実験数を効率よく省く手法だそうです。
例:直交表についての易しい具体例がのっていました
http://
以下の説明に使うこととします。
上記URLの内容としては、おいしいお茶を入れるには?ということで
A お茶の種類 B 使用する水 C お湯の温度 D 蒸し時間
の4因子をそれぞれについて3通り条件を変えて実験をしています。
全部の組合せのデータをとるとしたら3x3x3x3=81通りの
実験データをとらなければなりませんが
どの2因子についても、2因子間の組合せ9通りが必ず含まれる実験の組合せが、次の9回でできます。
1 番茶 水道水 60℃ 1分
2 番茶 浄水 80℃ 2分
3 番茶 自然水 100℃ 3分
4 煎茶 水道水 80℃ 3分
5 煎茶 浄水 100℃ 1分
6 煎茶 自然水 60℃ 2分
7 玉露 水道水 100℃ 2分
8 玉露 浄水 60℃ 3分
9 玉露 自然水 80℃ 1分
このの実験組合せを作る基になるのがL9直交表と
呼ばれるもので 次のようなものです。
No: ABCD
--------------
1: 1111
2: 1222
3: 1333
4; 2123
5: 2231
6: 2312
7: 3132
8: 3213
9: 3321
さて、この直交表は次のように並びかえることで、直交性や、魔方陣との関連を示すことができます。
上表のA列を下図の横の行に、B列を、下図の各列に割り当て、
(ここで、A列については、説明の便宜上 最下行を
最上行に循環シフトして3,1,2の順にしてあります)
C列の内容と D列の内容を枠内に収めます。
C D
┏-┳-┳-┓┏-┳-┳-┓ A
┃3┃1┃2┃┃2┃3┃1┃ ←3
┣-╋-╋-┫┣-╋-╋-┫
┃1┃2┃3┃┃1┃2┃3┃ ←1
┣-╋-╋-┫┣-╋-╋-┫
┃2┃3┃1┃┃3┃1┃2┃ ←2
┗-┻-┻-┛┗-┻-┻-┛
B↑1 2 3 1 2 3
・・・・直交表という言葉どおり、
枠内のCとDとが、各行、各列の
(つまり どのAとBに対しても)
どこにおいても、1から3までの要素が、
必ず含まれていることが判ります。
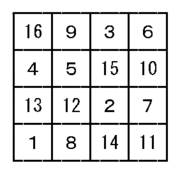
Dの表の1,2,3を 0,3,6に置き換えて、Cと(D-1)*3の和を
とると 下右図のように3方陣の完成です。
1から9までの数字が重複無く得られるということが
Cの因子とDの因子とが直交していて、9通りすべての
場合の組合せを、直交表が含んでいることを意味します。
┏---┳---┳---┓ → ┏-┳-┳-┓
┃3+3┃1+6┃2+0┃ → ┃6┃7┃2┃
┣---╋---╋---┫ → ┣-╋-╋-┫
┃1+0┃2+3┃3+6┃ → ┃1┃5┃9┃
┣---╋---╋---┫ → ┣-╋-╋-┫
┃2+6┃3+0┃1+3┃ → ┃8┃3┃4┃
┗---┻---┻---┛ → ┗-┻-┻-┛
直交表についてググると、いろいろみつかりました。
”統計に関するミニ知識初級編 ”
http://
”直交表とは... 直交表(実験計画法)”
http://
”直交表作成プログラム”
http://
”直交表って何が直交しているの?”
http://
・・・・が、これと、魔方陣との関係について言及しているところは、みつかりません、しかし、
L4、L8、L9、L18 といった直交表のLというのは
LATIN SQUAREに由来しているということです。
ラテン方格 (Wikipedia) ”・・・ラテン方陣ともいう”
http://
ラテン方陣でググると、ようやく魔方陣との関連が
でてきますし、 グラフ理論とか群論の話まででてきました。
http://
http://
http://
既に、魔方陣 ラテン方陣で検索した結果が
これだけ載っておりました。
http://
・・・・・・以上、直交表と魔方陣との関連でした。
ラテン方陣には、数独などのパズルや、直交表といった実益のある話がたくさんあるのに、魔方陣になると、すこし、マニアックな世界になってしまうのか、どうも、御利益のありそうな話にたどりつきません。 なんか、いいトピックのネタないでしょうかねぇ。。。。
これが、ラテン方陣に基づくもので、魔方陣に関係ありという話です。
(少しは、魔方陣にも、実用的な意味があることを示したいといったところです。)
直交表は、実験計画法や品質工学に、でてくる内容で複数因子間の組合せに漏れが無いようにしながら実験数を効率よく省く手法だそうです。
例:直交表についての易しい具体例がのっていました
http://
以下の説明に使うこととします。
上記URLの内容としては、おいしいお茶を入れるには?ということで
A お茶の種類 B 使用する水 C お湯の温度 D 蒸し時間
の4因子をそれぞれについて3通り条件を変えて実験をしています。
全部の組合せのデータをとるとしたら3x3x3x3=81通りの
実験データをとらなければなりませんが
どの2因子についても、2因子間の組合せ9通りが必ず含まれる実験の組合せが、次の9回でできます。
1 番茶 水道水 60℃ 1分
2 番茶 浄水 80℃ 2分
3 番茶 自然水 100℃ 3分
4 煎茶 水道水 80℃ 3分
5 煎茶 浄水 100℃ 1分
6 煎茶 自然水 60℃ 2分
7 玉露 水道水 100℃ 2分
8 玉露 浄水 60℃ 3分
9 玉露 自然水 80℃ 1分
このの実験組合せを作る基になるのがL9直交表と
呼ばれるもので 次のようなものです。
No: ABCD
--------------
1: 1111
2: 1222
3: 1333
4; 2123
5: 2231
6: 2312
7: 3132
8: 3213
9: 3321
さて、この直交表は次のように並びかえることで、直交性や、魔方陣との関連を示すことができます。
上表のA列を下図の横の行に、B列を、下図の各列に割り当て、
(ここで、A列については、説明の便宜上 最下行を
最上行に循環シフトして3,1,2の順にしてあります)
C列の内容と D列の内容を枠内に収めます。
C D
┏-┳-┳-┓┏-┳-┳-┓ A
┃3┃1┃2┃┃2┃3┃1┃ ←3
┣-╋-╋-┫┣-╋-╋-┫
┃1┃2┃3┃┃1┃2┃3┃ ←1
┣-╋-╋-┫┣-╋-╋-┫
┃2┃3┃1┃┃3┃1┃2┃ ←2
┗-┻-┻-┛┗-┻-┻-┛
B↑1 2 3 1 2 3
・・・・直交表という言葉どおり、
枠内のCとDとが、各行、各列の
(つまり どのAとBに対しても)
どこにおいても、1から3までの要素が、
必ず含まれていることが判ります。
Dの表の1,2,3を 0,3,6に置き換えて、Cと(D-1)*3の和を
とると 下右図のように3方陣の完成です。
1から9までの数字が重複無く得られるということが
Cの因子とDの因子とが直交していて、9通りすべての
場合の組合せを、直交表が含んでいることを意味します。
┏---┳---┳---┓ → ┏-┳-┳-┓
┃3+3┃1+6┃2+0┃ → ┃6┃7┃2┃
┣---╋---╋---┫ → ┣-╋-╋-┫
┃1+0┃2+3┃3+6┃ → ┃1┃5┃9┃
┣---╋---╋---┫ → ┣-╋-╋-┫
┃2+6┃3+0┃1+3┃ → ┃8┃3┃4┃
┗---┻---┻---┛ → ┗-┻-┻-┛
直交表についてググると、いろいろみつかりました。
”統計に関するミニ知識初級編 ”
http://
”直交表とは... 直交表(実験計画法)”
http://
”直交表作成プログラム”
http://
”直交表って何が直交しているの?”
http://
・・・・が、これと、魔方陣との関係について言及しているところは、みつかりません、しかし、
L4、L8、L9、L18 といった直交表のLというのは
LATIN SQUAREに由来しているということです。
ラテン方格 (Wikipedia) ”・・・ラテン方陣ともいう”
http://
ラテン方陣でググると、ようやく魔方陣との関連が
でてきますし、 グラフ理論とか群論の話まででてきました。
http://
http://
http://
既に、魔方陣 ラテン方陣で検索した結果が
これだけ載っておりました。
http://
・・・・・・以上、直交表と魔方陣との関連でした。
ラテン方陣には、数独などのパズルや、直交表といった実益のある話がたくさんあるのに、魔方陣になると、すこし、マニアックな世界になってしまうのか、どうも、御利益のありそうな話にたどりつきません。 なんか、いいトピックのネタないでしょうかねぇ。。。。
|
|
|
|
コメント(6)
ちょっと久々に色々調べてみたのでコメントを。
直行表というのは代数の世界でいう有限体というものの強く関連しています。体というのが加減乗除という演算が「うまく」定義されている集合のことです。
例えば「5で割った余り(0〜4)」に注目するとそれは自然な演算に対して体になります。ここで、自然な演算とは足したり掛けたりして5以上になったらそれを5で割った余りに注目するということです。
例えば(*は掛け算、%は余算記号)
3+4=2(7%5=2だから)
2*2=4
3*3=4(9%5=4だから)
4*4=1(16%5=1だから)
となります。割り算は掛けて1になる数と定義します。例えば
2*3=1
よって、2は3の逆数だし、3は2の逆数。
4は4自身が逆数です。(逆数を逆元とよびます)
5で割った余り(Z/5Z とか表現しますが)は要素の数が5個ということで、位数5の体と呼びます。
では同じように位数4の体が作れるでしょうか?これはZ/4Zでは無理なんです。なぜなら
2*2=0、3*3=0であり、0以外の2つの元を掛けると0になってしまう組み合わせがあります。このため2と3には逆元が存在しません。
「5は素数」なのでたまたまうまくいったのです。4は素数じゃないからこうはうまくいかないわけです。
じゃぁ位数が4の有限体は存在しないのでしょうか?これは結論から言うと答えはNOで、次のような定理があります。
有限体の位数は必ずp^n個であり、また位数p^n個の有限体は必ず存在する。
ここでpは素数で、^は冪記号です。つまり任意の素数の冪の要素数となる有限体は必ず存在するのです。4は2^2と表せるから存在します。6は2*3であり、素数の冪にはならないので、そのような有限体は存在しません。
直行表というのは代数の世界でいう有限体というものの強く関連しています。体というのが加減乗除という演算が「うまく」定義されている集合のことです。
例えば「5で割った余り(0〜4)」に注目するとそれは自然な演算に対して体になります。ここで、自然な演算とは足したり掛けたりして5以上になったらそれを5で割った余りに注目するということです。
例えば(*は掛け算、%は余算記号)
3+4=2(7%5=2だから)
2*2=4
3*3=4(9%5=4だから)
4*4=1(16%5=1だから)
となります。割り算は掛けて1になる数と定義します。例えば
2*3=1
よって、2は3の逆数だし、3は2の逆数。
4は4自身が逆数です。(逆数を逆元とよびます)
5で割った余り(Z/5Z とか表現しますが)は要素の数が5個ということで、位数5の体と呼びます。
では同じように位数4の体が作れるでしょうか?これはZ/4Zでは無理なんです。なぜなら
2*2=0、3*3=0であり、0以外の2つの元を掛けると0になってしまう組み合わせがあります。このため2と3には逆元が存在しません。
「5は素数」なのでたまたまうまくいったのです。4は素数じゃないからこうはうまくいかないわけです。
じゃぁ位数が4の有限体は存在しないのでしょうか?これは結論から言うと答えはNOで、次のような定理があります。
有限体の位数は必ずp^n個であり、また位数p^n個の有限体は必ず存在する。
ここでpは素数で、^は冪記号です。つまり任意の素数の冪の要素数となる有限体は必ず存在するのです。4は2^2と表せるから存在します。6は2*3であり、素数の冪にはならないので、そのような有限体は存在しません。
では具体的にp^nの有限体はどうやって作ればいいのか?それを説明します。
p^nの有限体は有限体を係数とする多項式環というのに強く関連しています。以下簡単にするため係数が0または1のモノすなわち位数2の有限体して話をすすめます。この有限体で2^nの位数の体を作れます。
この有限体は2で割った余りに注目しているわけだから
0+0=0
0+1=1
1+0=1
1+1=0
1*1=1
0*1=1*0=0*0=0
しかルールがないきわめて単純なものです。これを念頭においておいてください。
さて、多項式ていうのは
f(x) = x^4 + x^2 + 1
みたいなやつで、これを次数の少ない多項式(例えばg(x)=x^2+1とか)で割った余りというのを定義できます。
f(x) = h(x)g(x) + r(x)
とおくと、r(x)はg(x)より次数が少ない関数になり、整数におけるnで割った余りみたいなものが定義できるわけです。これがうまく定義できることは証明がいるんですがここでは省略します。
この条件で考えると面白いことがおきます。
0次式は 0,1のみ
1次式は x,x+1 のみ
です。これで4つの式が定義できます。2次式は全部で4種類あるんですが、1次式を掛け合わせると・・
x*x = x^2
x(x+1) = x^2+x
(x+1)(x+1) = x^2 + 1 (これは奇妙に見えるけど2x=(1+1)x=0x=0だからこの有限体の世界では正しい)
となり、x^2 + x + 1だけ現れません。これはすなわち「1次式で因数分解できない」ということにほかなりません。
これを実数係数の方程式と同様に「規約である」と定義します。逆を言えばこれ以外の2次式は1次式の積にできてしまうわけです。
このことから、任意の式f(x)を x^2+x+1で割った余りというのは 0,1,x,x+1のいずれかになるということが想像できるかと思います。実際そうなります。
「割った余り」というところでピンと来た人もいるかと思います。そう、この余りが位数4の有限体になっているのです。
例えば足し算は(0と足すという自明なものは省略している)
1+1=0
1+x=x+1
1+(x+1) = x
x+x = 0
x+(x+1) = 1
(x+1)+(x+1) = 0
掛け算は
x*x = x^2
x*(x+1) = x^2+x
(x+1)*(x+1) = (x^2 + 2x + 1) = x^2 + 1
となってしまいますが今回は x^2+x+1で割った余りに注目しているのだから、
x^2+x+1=0 → x^2=-(x+1) = x+1 と置き換えることができて、(1<=>-1として差し支えない)
x*x = x^2 = x+1
x*(x+1) = x^2+x = (x+1)+x = 1
(x+1)*(x+1) = (x^2 + 2x + 1) = x^2 + 1 = (x+1)+1 = x
となります。これらの演算表で逆元とかもうまく定義できます。
同じような考えでもっと次数の高い規約な式というのをどんどん定義できるのです。例えば
x^4+x+1
とか
x^16+x^12+x^5+1
とかです。前者は位数16の有限体、後者は位数256の有限体となります。
ちなみに後者の式はCRCというデータが正しいかどうかの検算によく使われるものです。
実は計算機の世界でよく使われるCRCっていうのと多項式環というのは密接な関係があるんですよ。
ここではすごく面倒な書き方をしているけど、2進数においてはシフト演算と排他的論理和(XOR)でCRCは簡単に計算できてしまうのです。
意外なところで意外なものが結びついているからあなどれませんねー
p^nの有限体は有限体を係数とする多項式環というのに強く関連しています。以下簡単にするため係数が0または1のモノすなわち位数2の有限体して話をすすめます。この有限体で2^nの位数の体を作れます。
この有限体は2で割った余りに注目しているわけだから
0+0=0
0+1=1
1+0=1
1+1=0
1*1=1
0*1=1*0=0*0=0
しかルールがないきわめて単純なものです。これを念頭においておいてください。
さて、多項式ていうのは
f(x) = x^4 + x^2 + 1
みたいなやつで、これを次数の少ない多項式(例えばg(x)=x^2+1とか)で割った余りというのを定義できます。
f(x) = h(x)g(x) + r(x)
とおくと、r(x)はg(x)より次数が少ない関数になり、整数におけるnで割った余りみたいなものが定義できるわけです。これがうまく定義できることは証明がいるんですがここでは省略します。
この条件で考えると面白いことがおきます。
0次式は 0,1のみ
1次式は x,x+1 のみ
です。これで4つの式が定義できます。2次式は全部で4種類あるんですが、1次式を掛け合わせると・・
x*x = x^2
x(x+1) = x^2+x
(x+1)(x+1) = x^2 + 1 (これは奇妙に見えるけど2x=(1+1)x=0x=0だからこの有限体の世界では正しい)
となり、x^2 + x + 1だけ現れません。これはすなわち「1次式で因数分解できない」ということにほかなりません。
これを実数係数の方程式と同様に「規約である」と定義します。逆を言えばこれ以外の2次式は1次式の積にできてしまうわけです。
このことから、任意の式f(x)を x^2+x+1で割った余りというのは 0,1,x,x+1のいずれかになるということが想像できるかと思います。実際そうなります。
「割った余り」というところでピンと来た人もいるかと思います。そう、この余りが位数4の有限体になっているのです。
例えば足し算は(0と足すという自明なものは省略している)
1+1=0
1+x=x+1
1+(x+1) = x
x+x = 0
x+(x+1) = 1
(x+1)+(x+1) = 0
掛け算は
x*x = x^2
x*(x+1) = x^2+x
(x+1)*(x+1) = (x^2 + 2x + 1) = x^2 + 1
となってしまいますが今回は x^2+x+1で割った余りに注目しているのだから、
x^2+x+1=0 → x^2=-(x+1) = x+1 と置き換えることができて、(1<=>-1として差し支えない)
x*x = x^2 = x+1
x*(x+1) = x^2+x = (x+1)+x = 1
(x+1)*(x+1) = (x^2 + 2x + 1) = x^2 + 1 = (x+1)+1 = x
となります。これらの演算表で逆元とかもうまく定義できます。
同じような考えでもっと次数の高い規約な式というのをどんどん定義できるのです。例えば
x^4+x+1
とか
x^16+x^12+x^5+1
とかです。前者は位数16の有限体、後者は位数256の有限体となります。
ちなみに後者の式はCRCというデータが正しいかどうかの検算によく使われるものです。
実は計算機の世界でよく使われるCRCっていうのと多項式環というのは密接な関係があるんですよ。
ここではすごく面倒な書き方をしているけど、2進数においてはシフト演算と排他的論理和(XOR)でCRCは簡単に計算できてしまうのです。
意外なところで意外なものが結びついているからあなどれませんねー
次に直行表について
これはあまゐりさんに以前日記にコメントでつけましたが、幾何の魔術という本に書いてあった手法をちょっと変えたものです。
グラフ用紙にX軸に4つ、Y軸に4つ目盛りをつけます。ただし、そこには0,1,2,3と振るのではなく、先ほど作成した位数4の有限体の要素、0,1、z、z+1とつけます。(平面グラフでx、yを多用するので間違えないように記号をzに置き換えました)
これで16個の点がグラフの上には現れます。ここで中学生で習った一次関数を思い出してください。そう
Y= A * X + B
てやつです。この関数でBを変化させるとそれはY軸における平行移動で、Bが異なる線は決して交差しません。これが位数4の有限体の上でも成立します。例えばA=1ならば
Y= X + 0
Y= X + 1
Y= X + z
Y= X + (z+1)
です。これはAがzとかz+1でも成立します。
Y= zX + 0
Y= zX + 1
Y= zX + z
Y= zX + (z+1)
Y= (z+1)X + 0
Y= (z+1)X + 1
Y= (z+1)X + z
Y= (z+1)X + (z+1)
なぜ成立するかというと体がうまく定義できているからなのです。これにA=0(すなわちX軸と平行な場合)ともう一セット
X=0, X=1, X=z, X=z+1というY軸に平行な直線を作ることができ、結局平行な4本の直線が5セットできることになります。
この5セットから任意の2セットをとってきますと、その組み合わせは直行します。A=1とA=zを試しに選んでみましょう。
A=1のときは
Y=X+BだからBが0,1,z,z+1の場合にXを0,1,z,z+1と変化させると
B=0: 0,1,z,z+1
B=1: 1,0,z+1,z
B=z: z,z+1,0,1
B=z+1: z+1,z,1,0
A=zのときは
Y=zX+Bだから
B=0: 0,z,z+1,1
B=1: 1,z+1,z,0
B=z: z,0,1,z+1
B=z+1: z+1,1,0,z
各ペアをもってくると
(0,0), (1,z), (z,z+1), (z+1,1)
(1,1), (0,z+1), (z+1,z), (z,0)
(z,z), (z+1,0), (0,1), (1,z+1)
(z+1,z+1), (z,1), (1,0), (0,z)
確かに16通りの組み合わせが全部現れています。軸に平行なつまらない直線をのぞく3つのセット(A=1,z,z+1)はすべて違う値が入っているから、ラテン方陣にもなります。
zを2、z+1を3としてみるとわかりやすいでしょう。
(0,0), (1,2), (2,3), (3,1)
(1,1), (0,3), (3,2), (2,0)
(2,2), (3,0), (0,1), (1,3)
(3,3), (2,1), (1,0), (0,2)
ペアのダブリなしで各列、各行に0〜3までの数字が入っているのがわかるかと思います。
なお、この手法でつくることができるラテン方陣はp^mのときだけですが、実際には2次と6次を除く次数のすべてのラテン方陣が存在することが既にわかっているそうです。
これはあまゐりさんに以前日記にコメントでつけましたが、幾何の魔術という本に書いてあった手法をちょっと変えたものです。
グラフ用紙にX軸に4つ、Y軸に4つ目盛りをつけます。ただし、そこには0,1,2,3と振るのではなく、先ほど作成した位数4の有限体の要素、0,1、z、z+1とつけます。(平面グラフでx、yを多用するので間違えないように記号をzに置き換えました)
これで16個の点がグラフの上には現れます。ここで中学生で習った一次関数を思い出してください。そう
Y= A * X + B
てやつです。この関数でBを変化させるとそれはY軸における平行移動で、Bが異なる線は決して交差しません。これが位数4の有限体の上でも成立します。例えばA=1ならば
Y= X + 0
Y= X + 1
Y= X + z
Y= X + (z+1)
です。これはAがzとかz+1でも成立します。
Y= zX + 0
Y= zX + 1
Y= zX + z
Y= zX + (z+1)
Y= (z+1)X + 0
Y= (z+1)X + 1
Y= (z+1)X + z
Y= (z+1)X + (z+1)
なぜ成立するかというと体がうまく定義できているからなのです。これにA=0(すなわちX軸と平行な場合)ともう一セット
X=0, X=1, X=z, X=z+1というY軸に平行な直線を作ることができ、結局平行な4本の直線が5セットできることになります。
この5セットから任意の2セットをとってきますと、その組み合わせは直行します。A=1とA=zを試しに選んでみましょう。
A=1のときは
Y=X+BだからBが0,1,z,z+1の場合にXを0,1,z,z+1と変化させると
B=0: 0,1,z,z+1
B=1: 1,0,z+1,z
B=z: z,z+1,0,1
B=z+1: z+1,z,1,0
A=zのときは
Y=zX+Bだから
B=0: 0,z,z+1,1
B=1: 1,z+1,z,0
B=z: z,0,1,z+1
B=z+1: z+1,1,0,z
各ペアをもってくると
(0,0), (1,z), (z,z+1), (z+1,1)
(1,1), (0,z+1), (z+1,z), (z,0)
(z,z), (z+1,0), (0,1), (1,z+1)
(z+1,z+1), (z,1), (1,0), (0,z)
確かに16通りの組み合わせが全部現れています。軸に平行なつまらない直線をのぞく3つのセット(A=1,z,z+1)はすべて違う値が入っているから、ラテン方陣にもなります。
zを2、z+1を3としてみるとわかりやすいでしょう。
(0,0), (1,2), (2,3), (3,1)
(1,1), (0,3), (3,2), (2,0)
(2,2), (3,0), (0,1), (1,3)
(3,3), (2,1), (1,0), (0,2)
ペアのダブリなしで各列、各行に0〜3までの数字が入っているのがわかるかと思います。
なお、この手法でつくることができるラテン方陣はp^mのときだけですが、実際には2次と6次を除く次数のすべてのラテン方陣が存在することが既にわかっているそうです。
応用編
16人でマージャン大会を行います。(マージャンというのは4人で遊ぶのですが)誰もが15人の人と一度対戦を行うように対戦の組み合わせをつくりたいですのですが、時間がないので最小試合数にしたい。いったいどう組めばよいでしょうか?
自分は常に3人を相手として戦い、相手の数は15人。うまくやれば同時進行4試合で、5回戦えば(都合20試合)終わりそうです。
これは先ほどのY=AX+Bの平行線で解決します。4*4の16個の交点に左下から0,1,2, ..., 15と番号をつけます。直線の上には4点乗るので、その人4人で戦えばOK。
第1ラウンド
Y=B
1卓 0,1,2,3
2卓 4,5,6,7
3卓 8,9,10,11
4卓 12,13,14,15
第2ラウンド
Y=A+B
1卓 0,5,10,15
2卓 1,4,11,14
3卓 2,7,8,13
4卓 3,6,9,12
第3ラウンド
Y=zA+B
1卓 0,6,11,13
2卓 1,7,10,12
3卓 2,4,9,15
4卓 3,5,8,14
第4ラウンド
Y=(z+1)A+B
1卓 0,7,9,14
2卓 1,6,8,15
3卓 2,5,11,12
4卓 3,4,10,13
第5ラウンドはY軸に平行な直線で
1卓 0,4,8,12
2卓 1,5,9,13
3卓 2,6,10,14
4卓 3,7,11,15
誰もが全員と必ず1回対戦してますよね?がんばってください。幹事さん。(笑)
16人でマージャン大会を行います。(マージャンというのは4人で遊ぶのですが)誰もが15人の人と一度対戦を行うように対戦の組み合わせをつくりたいですのですが、時間がないので最小試合数にしたい。いったいどう組めばよいでしょうか?
自分は常に3人を相手として戦い、相手の数は15人。うまくやれば同時進行4試合で、5回戦えば(都合20試合)終わりそうです。
これは先ほどのY=AX+Bの平行線で解決します。4*4の16個の交点に左下から0,1,2, ..., 15と番号をつけます。直線の上には4点乗るので、その人4人で戦えばOK。
第1ラウンド
Y=B
1卓 0,1,2,3
2卓 4,5,6,7
3卓 8,9,10,11
4卓 12,13,14,15
第2ラウンド
Y=A+B
1卓 0,5,10,15
2卓 1,4,11,14
3卓 2,7,8,13
4卓 3,6,9,12
第3ラウンド
Y=zA+B
1卓 0,6,11,13
2卓 1,7,10,12
3卓 2,4,9,15
4卓 3,5,8,14
第4ラウンド
Y=(z+1)A+B
1卓 0,7,9,14
2卓 1,6,8,15
3卓 2,5,11,12
4卓 3,4,10,13
第5ラウンドはY軸に平行な直線で
1卓 0,4,8,12
2卓 1,5,9,13
3卓 2,6,10,14
4卓 3,7,11,15
誰もが全員と必ず1回対戦してますよね?がんばってください。幹事さん。(笑)
- mixiユーザー
- ログインしてコメントしよう!
|
|
|
|
魔方陣について 更新情報
-
最新のイベント
-
まだ何もありません
-
-
最新のアンケート
-
まだ何もありません
-
魔方陣についてのメンバーはこんなコミュニティにも参加しています
人気コミュニティランキング
- 1位
- お洒落な女の子が好き
- 90059人
- 2位
- 酒好き
- 170693人
- 3位
- 写真を撮るのが好き
- 208291人