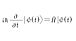4.4 流体粒子に対する運動量収支方程式と汚染物質に対する拡散方程式
流体粒子の大きさは直径が1ミクロンであるとしよう。流体粒子が連続体であるとみなしたから、1ミクロンの流体粒子の密度や速度や応力は絶対空間における任意の点Xの近傍でそれぞれの局所的な値を定義できた。しかしこの流体粒子の表面からは無数の微小な物質粒子や海水の分子が熱運動や乱流運動をしている。これらの流体粒子の運動が流体粒子を構成する微粒子の運動を表す収支方程式がまったく異なることを見てきた。まったく異なるという意味は一方がわかっても他方は全くわからないということである。したがってもし我々が流体粒子の運動量の収支方程式と密度の収支方程式を共存させたかったらならば、我々はこの両者が共存することを保証してやらなければならない。
「ニュートンの運動の第2法則で表現された流体粒子の運動は拡散方程式が存在する条件を満足するだろうか?」。換言すると拡散過程がガウス分布を満足することが観測で証明できたか?」と問う必要があるのである。
乱流観測データがガウス分布からははるかにずれることは指摘されてひさしい。
乱流の運動エネルギーeと平均の流速の空間的勾配Yとレイノルズ応力R=αeの観測データから経験法則
∂t( e ) = e ∇・U
を導き、右辺の∇Uは大規模平均流速の勾配とみなして
d( e ) = ( e − A) d U
と書き、これをeとUに関する完全微分型の微分方程式と思って解くと運動エネルギーとUは
Log (e −A) = U + Const.
になる。ここで大規模平均流速Uの分布がガウス分布にしたがう場合には乱流の運動エネルギーはガウス分布にならないでその対数がガウス分布になることがわかる(Landahl and Mollo-Christensen,1986)。また海洋表装の植物プランクトンと栄養塩分布もこのような正規分布にしたがう(Landahl and Mollo-Christensen,1986)。
実際に湖の表面に生じる波の乱流観測データはこのような対数ガウス分布になることが示された(Dorman and Mollo-Christensen、1973)。しかし対数ガウス分布もやはりその変数の逆数がガウス分布に依存することを仮定して導き出したものである。自然は本当にガウス分布を保証しているのだろうか?
4.5 アインシュタインの酔歩運動がわれわれに教えるもの
ミクロな水分子の熱振動が花粉の袋の中の微粒子に衝突し、その運動量が積算された微小時間εごとに微粒子が不規則に走り出す。これをブラウンはτ=30秒ごとに顕微鏡で観察したのであった。アインシュタインは微粒子がεごとに2次元平面を不規則に走り出す過程をちょうど泥酔者の千鳥足になぞらえて、2項分布で表現し、観測間隔τ=n・εとかき、nを10億としたのである。つまりn=10億回なら我々は泥酔者が過去を忘れて無限回の千鳥足を行ったとみなしたのである。
海洋表層の流体粒子の軌跡を人工衛星から観測することがある、1990年代はWOCE(世界海洋循環実験)という国際共同観測が実施され、西部熱帯海域で漂流浮きが放流され人その軌跡データが得られた。この軌跡をちょうどブラウン運動の軌跡と同じように見なして漂流浮きの乱流拡散による広がり幅を示す分散は幅は浮きの漂流時間の1.4乗である。環境汚染などのもとになる乱流拡散過程は十分に我々が理解したとはとてもいえない(Kiiedreich, Feng, Negel,2000)。ガウス分布よりも大きくずれる確率分布になることを実際の観測データが言っているのである(Metzer, Klafer, Sokolov,1998)。
したがって海洋表層の乱流拡散過程もブラウン運動型の拡散方程式では表現できないことを表しているのである。質点の運動方程式で表現される1ミクロンの大きさの流体粒子の連続な力学運動がナビエストークスの方程式で表現されるということと1ミクロンの大きさの流体粒子にくらべて非常に小さい熱力学的な物質の確率過程の運動とは何も関係がなかったのである。ミクロな確率過程が記憶を忘れた無限回の独立試行であるというのがブラウン運動の仮定であった。我々の気候予測モデルで採用している拡散過程はブラウン運動とまったく同じ構造をしているが、それでよいという保証はどこにもない。
質点の力学と両立する実際の海洋や大気における拡散過程は観測データによってその姿を発見されなければならない。
参考文献:
Dorman and Mollo-Christensen、1973:Observation of the structure of moving gust pattern over a water surface "Cat's paws". J. Phys. Oceanogr., 73, 120-413.
角谷典彦: 連続体力学、共立出版、1973
Kiiedreich, Feng, Negel,200:Nature, 403, 524.
Metzer, Klafer, Sokolov,1998::Phys. Rev., E., 58, 1621.
流体粒子の大きさは直径が1ミクロンであるとしよう。流体粒子が連続体であるとみなしたから、1ミクロンの流体粒子の密度や速度や応力は絶対空間における任意の点Xの近傍でそれぞれの局所的な値を定義できた。しかしこの流体粒子の表面からは無数の微小な物質粒子や海水の分子が熱運動や乱流運動をしている。これらの流体粒子の運動が流体粒子を構成する微粒子の運動を表す収支方程式がまったく異なることを見てきた。まったく異なるという意味は一方がわかっても他方は全くわからないということである。したがってもし我々が流体粒子の運動量の収支方程式と密度の収支方程式を共存させたかったらならば、我々はこの両者が共存することを保証してやらなければならない。
「ニュートンの運動の第2法則で表現された流体粒子の運動は拡散方程式が存在する条件を満足するだろうか?」。換言すると拡散過程がガウス分布を満足することが観測で証明できたか?」と問う必要があるのである。
乱流観測データがガウス分布からははるかにずれることは指摘されてひさしい。
乱流の運動エネルギーeと平均の流速の空間的勾配Yとレイノルズ応力R=αeの観測データから経験法則
∂t( e ) = e ∇・U
を導き、右辺の∇Uは大規模平均流速の勾配とみなして
d( e ) = ( e − A) d U
と書き、これをeとUに関する完全微分型の微分方程式と思って解くと運動エネルギーとUは
Log (e −A) = U + Const.
になる。ここで大規模平均流速Uの分布がガウス分布にしたがう場合には乱流の運動エネルギーはガウス分布にならないでその対数がガウス分布になることがわかる(Landahl and Mollo-Christensen,1986)。また海洋表装の植物プランクトンと栄養塩分布もこのような正規分布にしたがう(Landahl and Mollo-Christensen,1986)。
実際に湖の表面に生じる波の乱流観測データはこのような対数ガウス分布になることが示された(Dorman and Mollo-Christensen、1973)。しかし対数ガウス分布もやはりその変数の逆数がガウス分布に依存することを仮定して導き出したものである。自然は本当にガウス分布を保証しているのだろうか?
4.5 アインシュタインの酔歩運動がわれわれに教えるもの
ミクロな水分子の熱振動が花粉の袋の中の微粒子に衝突し、その運動量が積算された微小時間εごとに微粒子が不規則に走り出す。これをブラウンはτ=30秒ごとに顕微鏡で観察したのであった。アインシュタインは微粒子がεごとに2次元平面を不規則に走り出す過程をちょうど泥酔者の千鳥足になぞらえて、2項分布で表現し、観測間隔τ=n・εとかき、nを10億としたのである。つまりn=10億回なら我々は泥酔者が過去を忘れて無限回の千鳥足を行ったとみなしたのである。
海洋表層の流体粒子の軌跡を人工衛星から観測することがある、1990年代はWOCE(世界海洋循環実験)という国際共同観測が実施され、西部熱帯海域で漂流浮きが放流され人その軌跡データが得られた。この軌跡をちょうどブラウン運動の軌跡と同じように見なして漂流浮きの乱流拡散による広がり幅を示す分散は幅は浮きの漂流時間の1.4乗である。環境汚染などのもとになる乱流拡散過程は十分に我々が理解したとはとてもいえない(Kiiedreich, Feng, Negel,2000)。ガウス分布よりも大きくずれる確率分布になることを実際の観測データが言っているのである(Metzer, Klafer, Sokolov,1998)。
したがって海洋表層の乱流拡散過程もブラウン運動型の拡散方程式では表現できないことを表しているのである。質点の運動方程式で表現される1ミクロンの大きさの流体粒子の連続な力学運動がナビエストークスの方程式で表現されるということと1ミクロンの大きさの流体粒子にくらべて非常に小さい熱力学的な物質の確率過程の運動とは何も関係がなかったのである。ミクロな確率過程が記憶を忘れた無限回の独立試行であるというのがブラウン運動の仮定であった。我々の気候予測モデルで採用している拡散過程はブラウン運動とまったく同じ構造をしているが、それでよいという保証はどこにもない。
質点の力学と両立する実際の海洋や大気における拡散過程は観測データによってその姿を発見されなければならない。
参考文献:
Dorman and Mollo-Christensen、1973:Observation of the structure of moving gust pattern over a water surface "Cat's paws". J. Phys. Oceanogr., 73, 120-413.
角谷典彦: 連続体力学、共立出版、1973
Kiiedreich, Feng, Negel,200:Nature, 403, 524.
Metzer, Klafer, Sokolov,1998::Phys. Rev., E., 58, 1621.
|
|
|
|
コメント(1)
2月21日改訂版
ーーーーーーーーーーーーーーーーーーーーーーー
4.4 流体粒子に対する運動量収支方程式と汚染物質に対する拡散方程式
質点の運動方程式と物質の拡散方程式:
流体粒子の大きさは直径が1ミクロンであるとしよう(註2)。連続体としての流体粒子は、絶対空間の任意の点Xの近傍で1ミクロンの流体粒子の密度や速度や応力についてそれぞれ局所的な値を定義できる。流体粒子の表面からは無数の微小な物質粒子や海水の分子が熱運動や乱流運動をしている。
これらの流体粒子の連続な運動を表す運動量密度の収支方程式は流体粒子を構成する微粒子の不規則な確率運動を構成方程式とする密度の収支方程式とはまったく異なっていた。まったく異なるという意味は一方がわかっても他方は全くわからないということである。もし我々が流体粒子の運動量の収支方程式と密度の収支方程式を共存させたかったらならば、我々はこの両者が共存することを保証してやらなければならない。
それではニュートンの運動の第2法則で表現された流体粒子の運動は拡散方程式が存在する条件を満足するだろうか? 換言すると我々は「拡散過程がガウス分布を満足することが観測で証明できたか?」と問う必要があるのである。
ガウス分布から大きくずれた確率分布:
乱流観測データがガウス分布からははるかにずれることは指摘されてひさしい。
乱流の運動エネルギーeと平均の流速の空間的勾配Uとレイノルズ応力R=αeの観測データから得られた経験法則
∂t( e ) = e ∇・U
を導き、ここで右辺の∇Uを平均流速の勾配とみなして、等価な微分方程式
d( e ) = ( e − A) d U
に変換し、これをeとUに関する完全微分型の微分方程式と思って解くと乱流の運動エネルギーeと平均流速Uが満足する関係式
Log (e −A) = U + Const.
が得られる。ここで平均流速Uの分布がガウス分布にしたがう場合には乱流の運動エネルギーはガウス分布にならないでその対数がガウス分布になることがわかる(Landahl and Mollo-Christensen,1986)。また海洋表装の植物プランクトンと栄養塩分布もこのような正規分布にしたがう(Landahl and Mollo-Christensen,1986)。実際に湖の表面に生じる波の乱流観測データはこのような対数ガウス分布になることが示された(Dorman and Mollo-Christensen、1973)。しかし対数ガウス分布もやはりその変数の逆数がガウス分布に依存することを仮定して導き出したものである。自然は本当にガウス分布を保証しているのだろうか?
4.5 アインシュタインの酔歩運動がわれわれに教えるもの
ブラウン運動:
ミクロな水分子の熱振動が花粉の袋の中の微粒子に衝突し、その運動量が積算された微小時間εごとに微粒子が不規則に走り出す。これをブラウンはτ=30秒ごとに顕微鏡で観察したのであった。アインシュタインは微粒子がεごとに2次元平面を不規則に走り出す過程をちょうど泥酔者の千鳥足になぞらえて、2項分布で表現し、観測間隔τ=n・εとかき、nを10億としたのである。つまりn=10億回なら我々は泥酔者が過去を忘れて無限回の千鳥足を行ったとみなしたのである。
海洋表層の乱流による拡散:
海洋表層の流体粒子の軌跡を人工衛星から観測することがある、1990年代はWOCE(世界海洋循環実験)という国際共同観測が実施され、西部熱帯海域で漂流浮きが放流され人その軌跡データが得られた。この軌跡をちょうどブラウン運動の軌跡と同じように見なして漂流浮きの乱流拡散による広がり幅を示す分散は幅は浮きの漂流時間の1.4乗である。環境汚染などのもとになる乱流拡散過程は十分に我々が理解したとはとてもいえない(Kiiedreich, Feng, Negel,2000)。ガウス分布よりも大きくずれる確率分布になることを実際の観測データが言っているのである(Metzer, Klafer, Sokolov,1998)。したがって海洋表層の乱流拡散過程もブラウン運動型の拡散方程式では表現できないことを表しているのである。
乱流拡散と確率過程:
質点の運動方程式で表現される1ミクロンの大きさの流体粒子の連続な力学運動がナビエストークスの方程式で表現されるということと1ミクロンの大きさの流体粒子にくらべて非常に小さい熱力学的な物質の確率過程の運動とは何も関係がなかったのである。ミクロな確率過程が記憶を忘れた無限回の独立試行であるというのがブラウン運動の仮定であった。我々の気候予測モデルで採用している拡散過程はブラウン運動とまったく同じ構造をしているが、それでよいという保証はどこにもない。
質点の力学と両立する実際の海洋や大気における拡散過程は観測データによってその姿を発見されなければならない。
---------------------------------------------------------------------------------------------------------
註1:物理空間に埋め込まれ質点の幾何学を取り扱うためには位置を指定する基準が必要である。この基準を絶対静止基準とよぶことにする。ここで絶対という意味はどのような観測者からみても唯一の静止の基準がきまるということで、一義性(ユニーク)、一意性と言っても良い。絶対静止基準の原点に正座した観測者を絶対観測者と呼ぼう。
註2:ナ ビエストークスの方程式とは3次元空間の任意の領域で流体粒子の運動量密度の時間発展を決める方程式である。ここで3次元空間の任意の領域といったが、任 意の領域の場所と大きさを設定してやらなければいけない。まず流体粒子とは連続体の過程が成り立つ流体である。連続体とは時間軸と空間軸で最小の分割幅?tと?Xを目盛りにした最小の領域内で定義された物理量(密度や速度や温度)が、それよりも大きな時間空間領域にも連なっている(つまり連続している)ような物体である(バッチェラー、1972)。簡単に言うと物理量を定義できる最小の時間空間領域である。たとえば1ミクロン(10−6m)の立方体の水は連続体の仮定が成り立つ(大久保明、1985)。これからは海水の流体粒子の直径を1ミクロンとして議論していこう。参考のために、ブラウン運動をする花粉の中の微小粒子(これをブラウン粒子とよぼう)は直径が1ミクロンほどで、ブラウン粒子に衝突する水分子はその1000分の一から1万分の一の大きさである。
註3:絶対静止の基準から見た回転軸と回転方向を指定すれば地球の自転は決められる。地球の角速度ベクトルΩは地球の自転軸と自転運動を表す。角速度は時間がtだけ経過したとき回転座標上に固定された観測者Bが回転軸の周りを回転する角度θであるからΩ=dθ/dtである。ところが絶対静止の基準に正座している観測者Aは回転座標上に正座している観測者Bの変位角を−2θであると観測する。換言すれば絶対静止座標の中心Aを基準にすると回転座標上にいるBは2θだけ角変位を行っている。
ニュートンの運動方程式は絶対静止座標系で表現されなければならないから、絶対静止座標に正座した観測者Aにとって回転する座標系に固定されたBの単位時間当たりの変位角は2dθ/dt=2Ωである。
回転する円盤の中心に正座した絶対観測者Aが円盤の淵に立っている観測者Bに向けて外径の方向に初速度Vで質点を放り投げたとき、質点の運動方向に向かって右手の方向に加速度αを受けると考えると、質点の運動方程式を解くと質点の描く軌跡は放物線になり、外径と直角方向への移動距離をαt2/2を、円盤の淵に立つ目標Bの回転角ΩtとAからBまでの距離Vtを掛け算したものΩVt2に等しいとしてはいけない。なぜなら回転する円盤の中心は絶対座標(または慣性座標系)の中心ではないからである。ニュートンの運動の第2法則は常に絶対静止座標系または慣性座標系で使わなければならない。
註4:これが後に述べる質点の運動の第2法則で要求される絶対座標の存在を条件とする質点の力学と異なることである。つまり質点の運動の第2法則を公理系とする力学原理の枠組みの中では絶対座標の存在が必ず必要である。コリオリ力も波動の双方向伝播もこ質点の4次元時空幾何学をカーテシアン座標系を用いて表現するか、それとも座標系に依存しない数学形式で表現するかによって決まるのである。
絶対座標の存在を必要としないで物理量の全体としての調和と統一性を説いたライプニッツである。ライプニッツは物体の運動を、一物体の他物体に関しての単に相対的な移動であるとみなした(シュテインマン、1973)。これは毎回の移動が過去のしがらみから解放されて新たにサイコロを振って現在自分の位置を基準にして新たな出発を決めるブラウン運動の時空因果律を自己のうちに内包しているのである。ライプニッツが300年前に提案した半端な微分法(fractional derivatives)は現在ではガウス分布からずれた確率分布解を持つ確率微分方程式として発展している(Sokolov, Klafer, Blumen, 2002; Chatwin, 2003)
註5:これがアインシュタインの拡散過程に従う汚染物質濃度分布がガウス分布G( X.,t)になる根拠となる。
註6:気候シミュレーションに用いるナビエストークスの方程式では運動量密度ρvの密度を一定として音波を除去するのが普通である。つまり気象学は環境中の音波の伝播を取り扱ってこなかった。しかし沖縄県名護市辺野古集落の米軍キャンプシュワーブ基地の廃弾処理の衝撃で発生する音波は民家のコンクリート壁を破壊するのである(沖縄タイムス、2007年2月11日)。
註7:流体粒子が接している隣の流体粒子から受けるずれ応力などは近距離力である。海洋における異なる水塊や生物活動が原因となる海洋光学的な海水密度の擾乱による運動量密度の発生である。
参考文献:
Chawin, P., 2003:The Probability density function of concentration in atmospheric diffusion, 6th Internatinal Congress on Industrial and Applied Mathematics, Sydney, Australia, 7-11 July, 2003.
Dorman and Mollo-Christensen、1973:Observation of the structure of moving gust pattern over a water surface "Cat's paws". J. Phys. Oceanogr., 73, 120-413.
角谷典彦: 連続体力学、共立出版、1973
大久保明、1996:生物と流体、雑誌海洋と生物、37. Vol.7, No.3,123−125.
シュテインマン(水戸巌訳)、1973:時間と空間の物理学、東京出版
バッチェラー(橋本英典、松信八十男共訳)、1972:流体力学入門、東京電機大学出版
Kiiedreich, Feng, Negel,200:Nature, 403, 524.
Metzer, Klafer, Sokolov,1998::Phys. Rev., E., 58, 1621.
ーーーーーーーーーーーーーーーーーーーーーーー
4.4 流体粒子に対する運動量収支方程式と汚染物質に対する拡散方程式
質点の運動方程式と物質の拡散方程式:
流体粒子の大きさは直径が1ミクロンであるとしよう(註2)。連続体としての流体粒子は、絶対空間の任意の点Xの近傍で1ミクロンの流体粒子の密度や速度や応力についてそれぞれ局所的な値を定義できる。流体粒子の表面からは無数の微小な物質粒子や海水の分子が熱運動や乱流運動をしている。
これらの流体粒子の連続な運動を表す運動量密度の収支方程式は流体粒子を構成する微粒子の不規則な確率運動を構成方程式とする密度の収支方程式とはまったく異なっていた。まったく異なるという意味は一方がわかっても他方は全くわからないということである。もし我々が流体粒子の運動量の収支方程式と密度の収支方程式を共存させたかったらならば、我々はこの両者が共存することを保証してやらなければならない。
それではニュートンの運動の第2法則で表現された流体粒子の運動は拡散方程式が存在する条件を満足するだろうか? 換言すると我々は「拡散過程がガウス分布を満足することが観測で証明できたか?」と問う必要があるのである。
ガウス分布から大きくずれた確率分布:
乱流観測データがガウス分布からははるかにずれることは指摘されてひさしい。
乱流の運動エネルギーeと平均の流速の空間的勾配Uとレイノルズ応力R=αeの観測データから得られた経験法則
∂t( e ) = e ∇・U
を導き、ここで右辺の∇Uを平均流速の勾配とみなして、等価な微分方程式
d( e ) = ( e − A) d U
に変換し、これをeとUに関する完全微分型の微分方程式と思って解くと乱流の運動エネルギーeと平均流速Uが満足する関係式
Log (e −A) = U + Const.
が得られる。ここで平均流速Uの分布がガウス分布にしたがう場合には乱流の運動エネルギーはガウス分布にならないでその対数がガウス分布になることがわかる(Landahl and Mollo-Christensen,1986)。また海洋表装の植物プランクトンと栄養塩分布もこのような正規分布にしたがう(Landahl and Mollo-Christensen,1986)。実際に湖の表面に生じる波の乱流観測データはこのような対数ガウス分布になることが示された(Dorman and Mollo-Christensen、1973)。しかし対数ガウス分布もやはりその変数の逆数がガウス分布に依存することを仮定して導き出したものである。自然は本当にガウス分布を保証しているのだろうか?
4.5 アインシュタインの酔歩運動がわれわれに教えるもの
ブラウン運動:
ミクロな水分子の熱振動が花粉の袋の中の微粒子に衝突し、その運動量が積算された微小時間εごとに微粒子が不規則に走り出す。これをブラウンはτ=30秒ごとに顕微鏡で観察したのであった。アインシュタインは微粒子がεごとに2次元平面を不規則に走り出す過程をちょうど泥酔者の千鳥足になぞらえて、2項分布で表現し、観測間隔τ=n・εとかき、nを10億としたのである。つまりn=10億回なら我々は泥酔者が過去を忘れて無限回の千鳥足を行ったとみなしたのである。
海洋表層の乱流による拡散:
海洋表層の流体粒子の軌跡を人工衛星から観測することがある、1990年代はWOCE(世界海洋循環実験)という国際共同観測が実施され、西部熱帯海域で漂流浮きが放流され人その軌跡データが得られた。この軌跡をちょうどブラウン運動の軌跡と同じように見なして漂流浮きの乱流拡散による広がり幅を示す分散は幅は浮きの漂流時間の1.4乗である。環境汚染などのもとになる乱流拡散過程は十分に我々が理解したとはとてもいえない(Kiiedreich, Feng, Negel,2000)。ガウス分布よりも大きくずれる確率分布になることを実際の観測データが言っているのである(Metzer, Klafer, Sokolov,1998)。したがって海洋表層の乱流拡散過程もブラウン運動型の拡散方程式では表現できないことを表しているのである。
乱流拡散と確率過程:
質点の運動方程式で表現される1ミクロンの大きさの流体粒子の連続な力学運動がナビエストークスの方程式で表現されるということと1ミクロンの大きさの流体粒子にくらべて非常に小さい熱力学的な物質の確率過程の運動とは何も関係がなかったのである。ミクロな確率過程が記憶を忘れた無限回の独立試行であるというのがブラウン運動の仮定であった。我々の気候予測モデルで採用している拡散過程はブラウン運動とまったく同じ構造をしているが、それでよいという保証はどこにもない。
質点の力学と両立する実際の海洋や大気における拡散過程は観測データによってその姿を発見されなければならない。
---------------------------------------------------------------------------------------------------------
註1:物理空間に埋め込まれ質点の幾何学を取り扱うためには位置を指定する基準が必要である。この基準を絶対静止基準とよぶことにする。ここで絶対という意味はどのような観測者からみても唯一の静止の基準がきまるということで、一義性(ユニーク)、一意性と言っても良い。絶対静止基準の原点に正座した観測者を絶対観測者と呼ぼう。
註2:ナ ビエストークスの方程式とは3次元空間の任意の領域で流体粒子の運動量密度の時間発展を決める方程式である。ここで3次元空間の任意の領域といったが、任 意の領域の場所と大きさを設定してやらなければいけない。まず流体粒子とは連続体の過程が成り立つ流体である。連続体とは時間軸と空間軸で最小の分割幅?tと?Xを目盛りにした最小の領域内で定義された物理量(密度や速度や温度)が、それよりも大きな時間空間領域にも連なっている(つまり連続している)ような物体である(バッチェラー、1972)。簡単に言うと物理量を定義できる最小の時間空間領域である。たとえば1ミクロン(10−6m)の立方体の水は連続体の仮定が成り立つ(大久保明、1985)。これからは海水の流体粒子の直径を1ミクロンとして議論していこう。参考のために、ブラウン運動をする花粉の中の微小粒子(これをブラウン粒子とよぼう)は直径が1ミクロンほどで、ブラウン粒子に衝突する水分子はその1000分の一から1万分の一の大きさである。
註3:絶対静止の基準から見た回転軸と回転方向を指定すれば地球の自転は決められる。地球の角速度ベクトルΩは地球の自転軸と自転運動を表す。角速度は時間がtだけ経過したとき回転座標上に固定された観測者Bが回転軸の周りを回転する角度θであるからΩ=dθ/dtである。ところが絶対静止の基準に正座している観測者Aは回転座標上に正座している観測者Bの変位角を−2θであると観測する。換言すれば絶対静止座標の中心Aを基準にすると回転座標上にいるBは2θだけ角変位を行っている。
ニュートンの運動方程式は絶対静止座標系で表現されなければならないから、絶対静止座標に正座した観測者Aにとって回転する座標系に固定されたBの単位時間当たりの変位角は2dθ/dt=2Ωである。
回転する円盤の中心に正座した絶対観測者Aが円盤の淵に立っている観測者Bに向けて外径の方向に初速度Vで質点を放り投げたとき、質点の運動方向に向かって右手の方向に加速度αを受けると考えると、質点の運動方程式を解くと質点の描く軌跡は放物線になり、外径と直角方向への移動距離をαt2/2を、円盤の淵に立つ目標Bの回転角ΩtとAからBまでの距離Vtを掛け算したものΩVt2に等しいとしてはいけない。なぜなら回転する円盤の中心は絶対座標(または慣性座標系)の中心ではないからである。ニュートンの運動の第2法則は常に絶対静止座標系または慣性座標系で使わなければならない。
註4:これが後に述べる質点の運動の第2法則で要求される絶対座標の存在を条件とする質点の力学と異なることである。つまり質点の運動の第2法則を公理系とする力学原理の枠組みの中では絶対座標の存在が必ず必要である。コリオリ力も波動の双方向伝播もこ質点の4次元時空幾何学をカーテシアン座標系を用いて表現するか、それとも座標系に依存しない数学形式で表現するかによって決まるのである。
絶対座標の存在を必要としないで物理量の全体としての調和と統一性を説いたライプニッツである。ライプニッツは物体の運動を、一物体の他物体に関しての単に相対的な移動であるとみなした(シュテインマン、1973)。これは毎回の移動が過去のしがらみから解放されて新たにサイコロを振って現在自分の位置を基準にして新たな出発を決めるブラウン運動の時空因果律を自己のうちに内包しているのである。ライプニッツが300年前に提案した半端な微分法(fractional derivatives)は現在ではガウス分布からずれた確率分布解を持つ確率微分方程式として発展している(Sokolov, Klafer, Blumen, 2002; Chatwin, 2003)
註5:これがアインシュタインの拡散過程に従う汚染物質濃度分布がガウス分布G( X.,t)になる根拠となる。
註6:気候シミュレーションに用いるナビエストークスの方程式では運動量密度ρvの密度を一定として音波を除去するのが普通である。つまり気象学は環境中の音波の伝播を取り扱ってこなかった。しかし沖縄県名護市辺野古集落の米軍キャンプシュワーブ基地の廃弾処理の衝撃で発生する音波は民家のコンクリート壁を破壊するのである(沖縄タイムス、2007年2月11日)。
註7:流体粒子が接している隣の流体粒子から受けるずれ応力などは近距離力である。海洋における異なる水塊や生物活動が原因となる海洋光学的な海水密度の擾乱による運動量密度の発生である。
参考文献:
Chawin, P., 2003:The Probability density function of concentration in atmospheric diffusion, 6th Internatinal Congress on Industrial and Applied Mathematics, Sydney, Australia, 7-11 July, 2003.
Dorman and Mollo-Christensen、1973:Observation of the structure of moving gust pattern over a water surface "Cat's paws". J. Phys. Oceanogr., 73, 120-413.
角谷典彦: 連続体力学、共立出版、1973
大久保明、1996:生物と流体、雑誌海洋と生物、37. Vol.7, No.3,123−125.
シュテインマン(水戸巌訳)、1973:時間と空間の物理学、東京出版
バッチェラー(橋本英典、松信八十男共訳)、1972:流体力学入門、東京電機大学出版
Kiiedreich, Feng, Negel,200:Nature, 403, 524.
Metzer, Klafer, Sokolov,1998::Phys. Rev., E., 58, 1621.
- mixiユーザー
- ログインしてコメントしよう!
|
|
|
|
現代物理学史 更新情報
-
最新のイベント
-
最新のアンケート
-
まだ何もありません
-














![[dir]物理学全般](https://logo-imagecluster.img.mixi.jp/photo/comm/98/58/459858_7s.jpg)