>ラジアン表現で書くと、
>cos(π/2) + i sin(π/2) = i
>なので二倍するとπ/2になるのは、π/4と 5π/4
>cos(π/4) + i sin(π/4) は 1/√2 + i/√2
>cos(5π/4) + i sin(5π/4) は -1/√2 + (-i/√2)
>となり、AQさんの
>±1/√2 ± i/√2(複号同順)
>と同じ結果になります。
この議論を詳述すると、mode 計算をイメージできます。
かけ算は、指数にとっては足し算なので、
円を8等分する8の剰余系の足し算を考えます。
これは45度ずつの対応を考えることと同じ事なのが判ります。
0+0=0, 0+1=1, 0+2=2, 0+3=3, 0+4=4, 0+5=5, 0+6=6, 0+7=7,
1+0=1, 1+1=2, 1+2=3, 1+3=4, 1+4=5, 1+5=6, 1+6=7, 1+7=0,
2+0=2, 2+1=3, 2+2=4, 2+3=5, 2+4=6, 2+5=7, 2+6=0, 2+7=1,
3+0=3, 3+1=4, 3+2=5, 3+3=6, 3+4=7, 3+5=0, 3+6=1, 3+7=2,
4+0=4, 4+1=5, 4+2=6, 4+3=7, 4+4=0, 4+5=1, 4+6=2, 4+7=3,
5+0=5, 5+1=6, 5+2=7, 5+3=0, 5+4=1, 5+5=2, 5+6=3, 5+7=4,
6+0=6, 6+1=7, 6+2=8, 6+3=1, 6+4=2, 6+5=3, 6+6=4, 6+7=5,
7+0=7, 7+1=0, 7+2=1, 7+3=2, 7+4=3, 7+5=4, 7+6=5, 7+7=6,
ここで、同じ数を足して、2(90度)になるのは、1+1=2, 5+5=2,
因みに、-iを得るためには、同じ数を足して、6(270度)になればいいので、3+3=6, 7+7=6
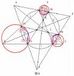
複素平面の単位円を8等分して、
1の8乗根ζ_8を考えます。 これをあらためて、ζとすると、
ζのかけ算は、上の表に従います。
ζ=cos(2π(1/8))+isin(2π(1/8))=cos(π/4)+isin(π/4)=1/√2+i/√2
ζ^5=cos(2π(5/8))+isin(2π(5/8))=cos(5π/4)+isin(5π/4)=-1/√2-i/√2
上の二つは、2乗してiになるもの、別に2乗して-iになるものを考えると
これは、4乗して-1になるもの、つまりは、x^4+1=0を満足していることがわかる。
x^4+1=(x^2+i)(x^2-i)=0
このx^4+1は、実数の範囲でこれ以上因数分解出来ないので、既約多項式である。
8乗根の場合の円周等分多項式というそうです。
>cos(π/2) + i sin(π/2) = i
>なので二倍するとπ/2になるのは、π/4と 5π/4
>cos(π/4) + i sin(π/4) は 1/√2 + i/√2
>cos(5π/4) + i sin(5π/4) は -1/√2 + (-i/√2)
>となり、AQさんの
>±1/√2 ± i/√2(複号同順)
>と同じ結果になります。
この議論を詳述すると、mode 計算をイメージできます。
かけ算は、指数にとっては足し算なので、
円を8等分する8の剰余系の足し算を考えます。
これは45度ずつの対応を考えることと同じ事なのが判ります。
0+0=0, 0+1=1, 0+2=2, 0+3=3, 0+4=4, 0+5=5, 0+6=6, 0+7=7,
1+0=1, 1+1=2, 1+2=3, 1+3=4, 1+4=5, 1+5=6, 1+6=7, 1+7=0,
2+0=2, 2+1=3, 2+2=4, 2+3=5, 2+4=6, 2+5=7, 2+6=0, 2+7=1,
3+0=3, 3+1=4, 3+2=5, 3+3=6, 3+4=7, 3+5=0, 3+6=1, 3+7=2,
4+0=4, 4+1=5, 4+2=6, 4+3=7, 4+4=0, 4+5=1, 4+6=2, 4+7=3,
5+0=5, 5+1=6, 5+2=7, 5+3=0, 5+4=1, 5+5=2, 5+6=3, 5+7=4,
6+0=6, 6+1=7, 6+2=8, 6+3=1, 6+4=2, 6+5=3, 6+6=4, 6+7=5,
7+0=7, 7+1=0, 7+2=1, 7+3=2, 7+4=3, 7+5=4, 7+6=5, 7+7=6,
ここで、同じ数を足して、2(90度)になるのは、1+1=2, 5+5=2,
因みに、-iを得るためには、同じ数を足して、6(270度)になればいいので、3+3=6, 7+7=6
複素平面の単位円を8等分して、
1の8乗根ζ_8を考えます。 これをあらためて、ζとすると、
ζのかけ算は、上の表に従います。
ζ=cos(2π(1/8))+isin(2π(1/8))=cos(π/4)+isin(π/4)=1/√2+i/√2
ζ^5=cos(2π(5/8))+isin(2π(5/8))=cos(5π/4)+isin(5π/4)=-1/√2-i/√2
上の二つは、2乗してiになるもの、別に2乗して-iになるものを考えると
これは、4乗して-1になるもの、つまりは、x^4+1=0を満足していることがわかる。
x^4+1=(x^2+i)(x^2-i)=0
このx^4+1は、実数の範囲でこれ以上因数分解出来ないので、既約多項式である。
8乗根の場合の円周等分多項式というそうです。
|
|
|
|
コメント(13)
いま、数論I(加藤和也、黒川重信、斎藤毅著)、初等整数論講義(高木貞治著)、といった本を中心に、代数幾何や数論、ゼータ関数などを理解しようと読んでいます。そうすると、複素数に関する基本的なことの理解が深まるように
感じています。
数には、整数(Z)、有理数(Q)、実数(R)、複素数(C)
とあって、古代ギリシャ数学は、有理数をもとにどう実数を正確に定義するか
悩んだのですが(√2が有理数で表せない)、それは19世紀末になって、Cantorが「収束すべき」数列(Cauchy列)の極限としての、実数の定義を考えて解決に至ったとのことです。それに先だって、Dedekindは「有理整数の集合の切断」としての、実数の定義を得ています。
さて、いま、数論に関係すると思われる、P進数なる違った数の概念を理解しようとしています。これは、1900年頃Henselによって導入された実数の世界を拡げた数になっているそうです。これは、いまでも完全に論理的な説明、証明が成されているわけではないとのことです。
P進数について書いた本の最初に以下の記述がありました。複素数について述べています。件の、x^2-i=0、が複素数の中で閉じていることは真に不思議でこれは、ガウスが何種類も証明を考えた代数学の基本定理というそうです。
P9 (p-adic Numbers, p-adic Analysis, and Zeta-Functions, by Neal Koblitz)
ここで、Rは実数、Cは複素数、p-adic NumbersはP進数、| |_p は、p進絶対値のこと。
Getting back to our historical survey, we've gotten as far as R. Next, returning to the first method - solving equations - mathematicians decided that it would be a good idea to have numbers that could solve equations like x^2+1=0. (This is taking things in logical order; historically speaking, the definition of the complex numbers came before the rigorous definition of the real numbers in terms of Cauchy sequences.) Then an amazing thing happened! As soon as i=√(-1) was introduced and the field of complex numbers of the form a+bi, a,b∈R, was defined, it turned out that:
(1)All polynominal equations with coefficients in C have solutions in C - this is the famous Fundamental Theorem of Algebra (the concise terminology is to say that C is algebraically closed); and
(2) C is already "complete" with respect to the (unique) norm which extends the norm | | on R (this norm is given by |a+bi|=√(a^2+b^2), i.e., any Cauchy sequence {a_j + b_ji} has a limit of the form a+bi (since {a_j}, and {b_j} will each be Cauchy sequences in R, you just let a and b their limits).
So the process stops with C, which is only a "quadratic extention" of R (i.e., obtained by adjoining a solution of the quadratic equation x^2+1=0). C is an algebraically closed field which is complete with respect to the Arichimedean metric.
But alas! Such is not to be the case with | |_p .......
複素数体C の重要な代数的性質は,C が代数的閉体であるということである.すなわち,C の元を係数とする任意の多項式f(x) に対して,代数方程式f(x)=0 は必ずC の中に解を持つ(C. F. Gaussに よる代数学の基本定理), 数学辞典第4版P394
複素数α=a+bi に対し,その絶対値(absolute value modulus)|α|を|a+bi|=√(a^2+b^2)=√αα'で定義する。α,βの距離ρ(α,β) を,ρ(α,β)=|α−β| によって定義すれば,ρ(α,β) は距離関数の公理を満たし,C は距離空間となる.この距離に関し,C は局所コンパクトで完備な距離空間である.数学辞典第4版P394
参考文献 数学辞典第4版P395
複素数の導入の歴史や応用については[2],1次変換については[1],[3].
[1]L. V. Ahlfors, Complex analysis, McGraw-Hill, 1953,(邦訳)複素解析, 現代数学社, 1982;[2]H.-D. Ebbinghaus 他編, Zahlen, Springer, 1983,(邦訳)数, 上・下, シュプリンガー・フェアラーク東京, 1991;
[3]L. R. Ford, Automorphic functions,McGraw-Hill, 1929(Chelsea, 1951).
感じています。
数には、整数(Z)、有理数(Q)、実数(R)、複素数(C)
とあって、古代ギリシャ数学は、有理数をもとにどう実数を正確に定義するか
悩んだのですが(√2が有理数で表せない)、それは19世紀末になって、Cantorが「収束すべき」数列(Cauchy列)の極限としての、実数の定義を考えて解決に至ったとのことです。それに先だって、Dedekindは「有理整数の集合の切断」としての、実数の定義を得ています。
さて、いま、数論に関係すると思われる、P進数なる違った数の概念を理解しようとしています。これは、1900年頃Henselによって導入された実数の世界を拡げた数になっているそうです。これは、いまでも完全に論理的な説明、証明が成されているわけではないとのことです。
P進数について書いた本の最初に以下の記述がありました。複素数について述べています。件の、x^2-i=0、が複素数の中で閉じていることは真に不思議でこれは、ガウスが何種類も証明を考えた代数学の基本定理というそうです。
P9 (p-adic Numbers, p-adic Analysis, and Zeta-Functions, by Neal Koblitz)
ここで、Rは実数、Cは複素数、p-adic NumbersはP進数、| |_p は、p進絶対値のこと。
Getting back to our historical survey, we've gotten as far as R. Next, returning to the first method - solving equations - mathematicians decided that it would be a good idea to have numbers that could solve equations like x^2+1=0. (This is taking things in logical order; historically speaking, the definition of the complex numbers came before the rigorous definition of the real numbers in terms of Cauchy sequences.) Then an amazing thing happened! As soon as i=√(-1) was introduced and the field of complex numbers of the form a+bi, a,b∈R, was defined, it turned out that:
(1)All polynominal equations with coefficients in C have solutions in C - this is the famous Fundamental Theorem of Algebra (the concise terminology is to say that C is algebraically closed); and
(2) C is already "complete" with respect to the (unique) norm which extends the norm | | on R (this norm is given by |a+bi|=√(a^2+b^2), i.e., any Cauchy sequence {a_j + b_ji} has a limit of the form a+bi (since {a_j}, and {b_j} will each be Cauchy sequences in R, you just let a and b their limits).
So the process stops with C, which is only a "quadratic extention" of R (i.e., obtained by adjoining a solution of the quadratic equation x^2+1=0). C is an algebraically closed field which is complete with respect to the Arichimedean metric.
But alas! Such is not to be the case with | |_p .......
複素数体C の重要な代数的性質は,C が代数的閉体であるということである.すなわち,C の元を係数とする任意の多項式f(x) に対して,代数方程式f(x)=0 は必ずC の中に解を持つ(C. F. Gaussに よる代数学の基本定理), 数学辞典第4版P394
複素数α=a+bi に対し,その絶対値(absolute value modulus)|α|を|a+bi|=√(a^2+b^2)=√αα'で定義する。α,βの距離ρ(α,β) を,ρ(α,β)=|α−β| によって定義すれば,ρ(α,β) は距離関数の公理を満たし,C は距離空間となる.この距離に関し,C は局所コンパクトで完備な距離空間である.数学辞典第4版P394
参考文献 数学辞典第4版P395
複素数の導入の歴史や応用については[2],1次変換については[1],[3].
[1]L. V. Ahlfors, Complex analysis, McGraw-Hill, 1953,(邦訳)複素解析, 現代数学社, 1982;[2]H.-D. Ebbinghaus 他編, Zahlen, Springer, 1983,(邦訳)数, 上・下, シュプリンガー・フェアラーク東京, 1991;
[3]L. R. Ford, Automorphic functions,McGraw-Hill, 1929(Chelsea, 1951).
続きです。
また、以下の7行は、数論Iの読書会の投稿からの写しです。
---------------------
奇素数pをとり、ζ=exp{2πi/p},K=Q(ζ)とおくと、
これは円分体と呼ばれる大変興味深い代数体が得られます。
最小多項式は
f(X)=X^{p−1}+X~{p-2}+…+X+1
で、K/QはAbel拡大であり、そのGalois群は
Gal(K/Q)〜(Z/pZ)^× (同型)
となり、分かりやすい面ももっています。
---------------------------
ここで、x^p=1を満足するので、
x^p-1=(x-1){X^{p−1}+X~{p-2}+…+X+1}=0
が成り立って、結局、自明なx=1を除くと、
f(X)=X^{p−1}+X~{p-2}+…+X+1=0
という関係が出てくる。
先の
cos(π/4) + i sin(π/4) は 1/√2 + i/√2
の例は、
素数では無いのですが、P'=8の場合です。
x^8-1=(x-1)(x^7+x^6+x^5+x^4+x^3+x^2+x+1)
=(x-1)(x+1)(x^2+1)(x^4+1)=0
(x-1)(x+1)(x^2+1)=0に関係する
自明なx=1.-1, i,-iを除くと、
x^4+1=0が残ります。
ここで出てくる、4つの数は、8の剰余系で考えると、
{1,3,5,7}に対応するものです。
因みに、
Gaussが、2次方程式を何段か重ねて解くことによって1の17乗根が得られることを「発見」し、これによって、彼は数学者になる決心をしたというのは
有名な話です。
自明な1を除くと16次の方程式が得られて、16=2^4、ですから、
これを8,4,2次式と半分ずつに解体していくことにより解ける。
これは、何回たどっても本当におもしろい解法ですね。
Gal(K/Q)はガロア拡大を表していて、円分体が、ガロア理論の代表的な
例になっていることが理解できます。
例えば、こんな議論が広がっていきます。
以下も読書会からの投稿のものです。
Q(ζ_8)の部分体をすべて挙げよ。それぞれの体において
完全分解する素数はなにか。という
数論Iの演習問題5.1の解答
-------------------------------------------
以下、ζ_8=ζとおく。1の原始8乗根はζ,ζ^3,ζ^5,ζ^7であり、
既約なf(x)=x^4+1∈Q[x]の根である。
σ,τ∈G=Gal(Q(ζ)/Q)をσ(ζ)=ζ^3,τ(ζ)=ζ^5で定義すると、
στ(ζ)=(ζ^5)^3=ζ^15=ζ^7,τσ(ζ)=(ζ^3)^5=ζ^15=ζ^7から、στ=τσ
従って、G=<σ,τ|σ^2=τ^2=1,στ=τσ>はアーベル群であり、部分群列は、
G⊃H={σ,1}⊃{1}
G⊃I={τ,1}⊃{1}
G⊃J={τσ,1}⊃{1}
Q(ζ)のQに対する拡大次数が4であることから、
Q上基底をζ,ζ^2,ζ^3,ζ^4
【G⊃H={σ,1}⊃{1}に対応するQ(ζ)の部分体列】
ζ-ζ^-1は、Hの同型写像により、固定されるから、
Hに対応するQとQ(ζ)の中間体はQ(ζ-ζ^-1)である。
【G⊃I⊃{1}に対応するQ(ζ)の部分体列】
τ(ζ^2)=ζ^10=ζ^2
即ちζ^2は、Iの同型写像により、固定されるから、
Iに対応するQとQ(ζ)の中間体はQ(ζ^2)である。
【G⊃J⊃{1}に対応するQ(ζ)の部分体列】
同様に、中間体Q(ζ+ζ^-1)を得る。
【まとめ】ζ^4=-1からQ(ζ^2)=Q(√-1)
(ζ+ζ^-1)^2+(ζ-ζ^-1)^2=2(ζ^2+ζ^-2)=0,(ζ+ζ^-1)^2-(ζ-ζ^-1)^2=4
から、(ζ+ζ^-1)^2=2,(ζ-ζ^-1)^2=-2を得る。
従って、Q(ζ+ζ^-1)=Q(√2),Q(ζ-ζ^-1)=Q(√-2)であり、
Q(ζ_8)の部分体列は、
Q(ζ_8)⊃Q(√-2)⊃Q,
Q(ζ_8)⊃Q(√-1)⊃Q,
Q(ζ_8)⊃Q(√2)⊃Qの3通りある。
更に、Gは{1,3,5,7},Hは{1,3},Iは{1,5},Jは{1,7}
と同一視出来るので、
Gal(Q(ζ_8)/Q(ζ_8))={1}から、Q(ζ_8)はp≡1 mod 8
Gal(Q(ζ_8)/Q(√-2))=Hから、Q(√-2)はp≡1,3 mod 8
Gal(Q(ζ_8)/Q(√-1))=Iから、Q(√-1)はp≡1,5 mod 8
(p≡1 mod 4でもある。)
Gal(Q(ζ_8)/Q(√2))=Jから、Q(√2)はp≡1,7 mod 8
Gal(Q(ζ_8)/Q)=Gから、Qはp≡1,3,5,7 mod 8従って、全ての素数
を完全分解する。
-----------------------------------------
また、以下の7行は、数論Iの読書会の投稿からの写しです。
---------------------
奇素数pをとり、ζ=exp{2πi/p},K=Q(ζ)とおくと、
これは円分体と呼ばれる大変興味深い代数体が得られます。
最小多項式は
f(X)=X^{p−1}+X~{p-2}+…+X+1
で、K/QはAbel拡大であり、そのGalois群は
Gal(K/Q)〜(Z/pZ)^× (同型)
となり、分かりやすい面ももっています。
---------------------------
ここで、x^p=1を満足するので、
x^p-1=(x-1){X^{p−1}+X~{p-2}+…+X+1}=0
が成り立って、結局、自明なx=1を除くと、
f(X)=X^{p−1}+X~{p-2}+…+X+1=0
という関係が出てくる。
先の
cos(π/4) + i sin(π/4) は 1/√2 + i/√2
の例は、
素数では無いのですが、P'=8の場合です。
x^8-1=(x-1)(x^7+x^6+x^5+x^4+x^3+x^2+x+1)
=(x-1)(x+1)(x^2+1)(x^4+1)=0
(x-1)(x+1)(x^2+1)=0に関係する
自明なx=1.-1, i,-iを除くと、
x^4+1=0が残ります。
ここで出てくる、4つの数は、8の剰余系で考えると、
{1,3,5,7}に対応するものです。
因みに、
Gaussが、2次方程式を何段か重ねて解くことによって1の17乗根が得られることを「発見」し、これによって、彼は数学者になる決心をしたというのは
有名な話です。
自明な1を除くと16次の方程式が得られて、16=2^4、ですから、
これを8,4,2次式と半分ずつに解体していくことにより解ける。
これは、何回たどっても本当におもしろい解法ですね。
Gal(K/Q)はガロア拡大を表していて、円分体が、ガロア理論の代表的な
例になっていることが理解できます。
例えば、こんな議論が広がっていきます。
以下も読書会からの投稿のものです。
Q(ζ_8)の部分体をすべて挙げよ。それぞれの体において
完全分解する素数はなにか。という
数論Iの演習問題5.1の解答
-------------------------------------------
以下、ζ_8=ζとおく。1の原始8乗根はζ,ζ^3,ζ^5,ζ^7であり、
既約なf(x)=x^4+1∈Q[x]の根である。
σ,τ∈G=Gal(Q(ζ)/Q)をσ(ζ)=ζ^3,τ(ζ)=ζ^5で定義すると、
στ(ζ)=(ζ^5)^3=ζ^15=ζ^7,τσ(ζ)=(ζ^3)^5=ζ^15=ζ^7から、στ=τσ
従って、G=<σ,τ|σ^2=τ^2=1,στ=τσ>はアーベル群であり、部分群列は、
G⊃H={σ,1}⊃{1}
G⊃I={τ,1}⊃{1}
G⊃J={τσ,1}⊃{1}
Q(ζ)のQに対する拡大次数が4であることから、
Q上基底をζ,ζ^2,ζ^3,ζ^4
【G⊃H={σ,1}⊃{1}に対応するQ(ζ)の部分体列】
ζ-ζ^-1は、Hの同型写像により、固定されるから、
Hに対応するQとQ(ζ)の中間体はQ(ζ-ζ^-1)である。
【G⊃I⊃{1}に対応するQ(ζ)の部分体列】
τ(ζ^2)=ζ^10=ζ^2
即ちζ^2は、Iの同型写像により、固定されるから、
Iに対応するQとQ(ζ)の中間体はQ(ζ^2)である。
【G⊃J⊃{1}に対応するQ(ζ)の部分体列】
同様に、中間体Q(ζ+ζ^-1)を得る。
【まとめ】ζ^4=-1からQ(ζ^2)=Q(√-1)
(ζ+ζ^-1)^2+(ζ-ζ^-1)^2=2(ζ^2+ζ^-2)=0,(ζ+ζ^-1)^2-(ζ-ζ^-1)^2=4
から、(ζ+ζ^-1)^2=2,(ζ-ζ^-1)^2=-2を得る。
従って、Q(ζ+ζ^-1)=Q(√2),Q(ζ-ζ^-1)=Q(√-2)であり、
Q(ζ_8)の部分体列は、
Q(ζ_8)⊃Q(√-2)⊃Q,
Q(ζ_8)⊃Q(√-1)⊃Q,
Q(ζ_8)⊃Q(√2)⊃Qの3通りある。
更に、Gは{1,3,5,7},Hは{1,3},Iは{1,5},Jは{1,7}
と同一視出来るので、
Gal(Q(ζ_8)/Q(ζ_8))={1}から、Q(ζ_8)はp≡1 mod 8
Gal(Q(ζ_8)/Q(√-2))=Hから、Q(√-2)はp≡1,3 mod 8
Gal(Q(ζ_8)/Q(√-1))=Iから、Q(√-1)はp≡1,5 mod 8
(p≡1 mod 4でもある。)
Gal(Q(ζ_8)/Q(√2))=Jから、Q(√2)はp≡1,7 mod 8
Gal(Q(ζ_8)/Q)=Gから、Qはp≡1,3,5,7 mod 8従って、全ての素数
を完全分解する。
-----------------------------------------
今回は、ここまでです。
-------------------------
ζ_8については、
こんなのもありました。数論IのP105演習問題3.3
ζ_8= cos(π/4) + i sin(π/4)=(1+i)/√2,
とし、a=1,3,5,7に対し、
s_a=Σ[n=1,∞]{ζ_8^(an)}/n= -log {1-ζ_8^(a)} と置く。
s_1-s_3-s_5+s_7を計算することにより、
1-1/3-1/5+1/7+1/9-1/11-1/13+1/15
+---(正負の符号は8ごとに繰り返す)
=(1/√2)log(1+√2)
の公式を証明せよ。(Dirichletの公式)
---------
L(1, χ)=Σ[n=1,∞]χ(n)/n
と置きこれをχについてのDirichlet L関数と呼ぶ。
ここでχ(n)はDirichlet指標
χ(1 mod 8)=χ(7 mod 8)=1, χ(3 mod 8)=χ(5 mod 8)=-1
s_1-s_3-s_5+s_7
= -log{1-ζ_8}{1-ζ_8^(7)}/{1-ζ_8^(3)}{1-ζ_8^(5)} ?
ζ_8= (1+i)/√2, ζ_8^(3)=(-1+i)/√2
ζ_8^(5)=(-1-i)/√2, ζ_8^(7)= (1-i)/√2
を?に代入すると
s_1-s_3-s_5+s_7 = 2 log(1+√2) ?
一方:
s_1-s_3-s_5+s_7
={ζ_8-ζ_8^(3)-ζ_8(5)+ζ_8^(7)}Σ[n=1,∞]χ(n)/n ?
ζ_8-ζ_8^(3)-ζ_8(5)+ζ_8^(7)
=(1+i)/√2-(-1+i)/√2-(-1-i)/√2+(1-i)/√2 = 2√2
なので、 ?に代入して、
s_1-s_3-s_5+s_7=2√2*L(1, χ) ?
??より、L(1, χ)=(1/√2)log(1+√2)
-----------------------
長くなりました。
こういったことが、発見といえるのか、発明といえるのか。
知人のひとりは、夏目漱石の夢十夜、運慶の文章を紹介しています。
「能くああ無造作に鑿を使って、思う様な眉や鼻ができるものだな」と自
分はあんまり感心したから独言の様に言った。するとさっきの若い男が、
「なに、あれは眉や鼻を鑿で作るんじゃない。あの通りの眉や鼻が木の中
に埋っているのを、鑿と槌の力で掘り出すまでだ。まるで土の中から石を
掘り出す様なものだから決して間違う筈はない」と云った。
-------------------------
ζ_8については、
こんなのもありました。数論IのP105演習問題3.3
ζ_8= cos(π/4) + i sin(π/4)=(1+i)/√2,
とし、a=1,3,5,7に対し、
s_a=Σ[n=1,∞]{ζ_8^(an)}/n= -log {1-ζ_8^(a)} と置く。
s_1-s_3-s_5+s_7を計算することにより、
1-1/3-1/5+1/7+1/9-1/11-1/13+1/15
+---(正負の符号は8ごとに繰り返す)
=(1/√2)log(1+√2)
の公式を証明せよ。(Dirichletの公式)
---------
L(1, χ)=Σ[n=1,∞]χ(n)/n
と置きこれをχについてのDirichlet L関数と呼ぶ。
ここでχ(n)はDirichlet指標
χ(1 mod 8)=χ(7 mod 8)=1, χ(3 mod 8)=χ(5 mod 8)=-1
s_1-s_3-s_5+s_7
= -log{1-ζ_8}{1-ζ_8^(7)}/{1-ζ_8^(3)}{1-ζ_8^(5)} ?
ζ_8= (1+i)/√2, ζ_8^(3)=(-1+i)/√2
ζ_8^(5)=(-1-i)/√2, ζ_8^(7)= (1-i)/√2
を?に代入すると
s_1-s_3-s_5+s_7 = 2 log(1+√2) ?
一方:
s_1-s_3-s_5+s_7
={ζ_8-ζ_8^(3)-ζ_8(5)+ζ_8^(7)}Σ[n=1,∞]χ(n)/n ?
ζ_8-ζ_8^(3)-ζ_8(5)+ζ_8^(7)
=(1+i)/√2-(-1+i)/√2-(-1-i)/√2+(1-i)/√2 = 2√2
なので、 ?に代入して、
s_1-s_3-s_5+s_7=2√2*L(1, χ) ?
??より、L(1, χ)=(1/√2)log(1+√2)
-----------------------
長くなりました。
こういったことが、発見といえるのか、発明といえるのか。
知人のひとりは、夏目漱石の夢十夜、運慶の文章を紹介しています。
「能くああ無造作に鑿を使って、思う様な眉や鼻ができるものだな」と自
分はあんまり感心したから独言の様に言った。するとさっきの若い男が、
「なに、あれは眉や鼻を鑿で作るんじゃない。あの通りの眉や鼻が木の中
に埋っているのを、鑿と槌の力で掘り出すまでだ。まるで土の中から石を
掘り出す様なものだから決して間違う筈はない」と云った。
1,3,5,7は8の原始根になっています。
原始根とは、2乗、3乗、、としていって
全ての数を渡り歩き、8乗して始めて1になるもの。
ζ,ζ^2,ζ^3,ζ^4,ζ^5,ζ^6,ζ^7,ζ^8=1
ζ^3,
(ζ^3)^2=ζ^6,
(ζ^3)^3=ζ^9=ζ^(8+1)=ζ
(ζ^3)^4=ζ^12=ζ^(8+4)=ζ^4
(ζ^3)^5=ζ^15=ζ^(8+7)=ζ^7
(ζ^3)^6=ζ^18=ζ^(2*8+2)=ζ^2
(ζ^3)^7=ζ^21=ζ^(2*8+5)=ζ^5
(ζ^3)^8=ζ^24=ζ^(3*8+3)=ζ^8=ζ^0=1
ζ^5,
(ζ^5)^2=ζ^10=ζ^(8+2)=ζ^2
(ζ^5)^3=ζ^15=ζ^(8+7)=ζ^7
(ζ^5)^4=ζ^20=ζ^(2*8+4)=ζ^4
(ζ^5)^5=ζ^25=ζ^(3*8+1)=ζ
(ζ^5)^6=ζ^30=ζ^(3*8+6)=ζ^6
(ζ^5)^7=ζ^35=ζ^(4*8+3)=ζ^3
(ζ^5)^8=ζ^24=ζ^(3*8)=ζ^8=ζ^0=1
ζ^7,
(ζ^7)^2=ζ^14=ζ^(8+6)=ζ^6
(ζ^7)^3=ζ^21=ζ^(2*8+5)=ζ^5
(ζ^7)^4=ζ^28=ζ^(3*8+4)=ζ^4
(ζ^7)^5=ζ^35=ζ^(4*8+3)=ζ^3
(ζ^7)^6=ζ^42=ζ^(5*8+2)=ζ^2
(ζ^7)^7=ζ^49=ζ^(6*8+1)=ζ
(ζ^7)^8=ζ^56=ζ^(7*8)=ζ^0=1
指数の所を見てみる。
ζ :1,2,3,4,5,6,7,8=0
ζ^3:3,6,1,4,7,2,5,8=0
ζ^5:5,2,7,4,1,6,3,8=0
ζ^7:7,6,5,4,3,2,1,8=0
x^8-1=0を展開すると、
x^8-1
=(x-1)(x+1)(x^2+1)(x^4+1)
ここで、x=1,-1,i,-iは原始根にならない。
x^4+1=0の解だけ、原始根になる。
原始根とは、2乗、3乗、、としていって
全ての数を渡り歩き、8乗して始めて1になるもの。
ζ,ζ^2,ζ^3,ζ^4,ζ^5,ζ^6,ζ^7,ζ^8=1
ζ^3,
(ζ^3)^2=ζ^6,
(ζ^3)^3=ζ^9=ζ^(8+1)=ζ
(ζ^3)^4=ζ^12=ζ^(8+4)=ζ^4
(ζ^3)^5=ζ^15=ζ^(8+7)=ζ^7
(ζ^3)^6=ζ^18=ζ^(2*8+2)=ζ^2
(ζ^3)^7=ζ^21=ζ^(2*8+5)=ζ^5
(ζ^3)^8=ζ^24=ζ^(3*8+3)=ζ^8=ζ^0=1
ζ^5,
(ζ^5)^2=ζ^10=ζ^(8+2)=ζ^2
(ζ^5)^3=ζ^15=ζ^(8+7)=ζ^7
(ζ^5)^4=ζ^20=ζ^(2*8+4)=ζ^4
(ζ^5)^5=ζ^25=ζ^(3*8+1)=ζ
(ζ^5)^6=ζ^30=ζ^(3*8+6)=ζ^6
(ζ^5)^7=ζ^35=ζ^(4*8+3)=ζ^3
(ζ^5)^8=ζ^24=ζ^(3*8)=ζ^8=ζ^0=1
ζ^7,
(ζ^7)^2=ζ^14=ζ^(8+6)=ζ^6
(ζ^7)^3=ζ^21=ζ^(2*8+5)=ζ^5
(ζ^7)^4=ζ^28=ζ^(3*8+4)=ζ^4
(ζ^7)^5=ζ^35=ζ^(4*8+3)=ζ^3
(ζ^7)^6=ζ^42=ζ^(5*8+2)=ζ^2
(ζ^7)^7=ζ^49=ζ^(6*8+1)=ζ
(ζ^7)^8=ζ^56=ζ^(7*8)=ζ^0=1
指数の所を見てみる。
ζ :1,2,3,4,5,6,7,8=0
ζ^3:3,6,1,4,7,2,5,8=0
ζ^5:5,2,7,4,1,6,3,8=0
ζ^7:7,6,5,4,3,2,1,8=0
x^8-1=0を展開すると、
x^8-1
=(x-1)(x+1)(x^2+1)(x^4+1)
ここで、x=1,-1,i,-iは原始根にならない。
x^4+1=0の解だけ、原始根になる。
>Gal(Q(ζ_8)/Q(ζ_8))={1}から、Q(ζ_8)はp≡1 mod 8
>Gal(Q(ζ_8)/Q(√-2))=Hから、Q(√-2)はp≡1,3 mod 8
>Gal(Q(ζ_8)/Q(√-1))=Iから、Q(√-1)はp≡1,5 mod 8
(p≡1 mod 4でもある。)
>Gal(Q(ζ_8)/Q(√2))=Jから、Q(√2)はp≡1,7 mod 8
>Gal(Q(ζ_8)/Q)=Gから、Qはp≡1,3,5,7 mod 8従って、全ての素数
を完全分解する。
は何をいっているのか。
Q(√-2)はp≡1,3 mod 8
例:11=(√2+3√(-1))(√2-3√(-1))
Q(√-1)はp≡1,5 mod 8 (p≡1 mod 4でもある。)
例:5=(2+√(-1))(2-√(-1))
Q(√2)はp≡1,7 mod 8
例:17=(2√2+3)(-2√2+3)
------------数論Iのp143、144
-------------------------------------
Kを代数体、Lをその有限次拡大とする。
Kの整数環O_kのゼロでない素イデアル(「Kの素イデアル」と略称する)
がLにおいてどう分解するかは、大切なことであり、その分解の様子について
「分岐、不分岐、完全分解」という用語を使う。
pをO_kの0でない素イデアルとし、
O_Lpを、pが生成するO_Lの素イデアルとする。
(5.1) O_Lpは、O_Lp=q_1^(e_1)...q_g^(e_g)
の形にあらわされる。
q_1,...,q_gはO_Lの相異なる0でない素イデアル、e_i≧1
e_1=...=^(e_g)=1であるとき、pはLにおいて不分岐(unramified)であるという。不分岐でないとき、すなわちあるiについてe_i≧2であるとき、
pはLにおいて分岐(ramified)であるという。
例えば、K=Q,L=Q(√(-1))
のとき、Lにおいて分岐するZの0でない素イデアルは2Zのみである。
一般に(5.1)について、
(5.2) ?[i=1,g] e_i ≦ [L:K]
([L:K]は体の拡大次数)であること、したがって、とくにg≦[L:K]であることが
しられている。
定義5.3
O_Lpが、[L:K]個のO_Lの相異なる0でない素イデアルの積となるとき、すなわちg=[L:K] であるとき、pはLにおいて完全分解するという。
完全分解すれば不分岐である。
-------------------------------
--------------------------
>Gal(Q(ζ_8)/Q(√-2))=Hから、Q(√-2)はp≡1,3 mod 8
>Gal(Q(ζ_8)/Q(√-1))=Iから、Q(√-1)はp≡1,5 mod 8
(p≡1 mod 4でもある。)
>Gal(Q(ζ_8)/Q(√2))=Jから、Q(√2)はp≡1,7 mod 8
>Gal(Q(ζ_8)/Q)=Gから、Qはp≡1,3,5,7 mod 8従って、全ての素数
を完全分解する。
は何をいっているのか。
Q(√-2)はp≡1,3 mod 8
例:11=(√2+3√(-1))(√2-3√(-1))
Q(√-1)はp≡1,5 mod 8 (p≡1 mod 4でもある。)
例:5=(2+√(-1))(2-√(-1))
Q(√2)はp≡1,7 mod 8
例:17=(2√2+3)(-2√2+3)
------------数論Iのp143、144
-------------------------------------
Kを代数体、Lをその有限次拡大とする。
Kの整数環O_kのゼロでない素イデアル(「Kの素イデアル」と略称する)
がLにおいてどう分解するかは、大切なことであり、その分解の様子について
「分岐、不分岐、完全分解」という用語を使う。
pをO_kの0でない素イデアルとし、
O_Lpを、pが生成するO_Lの素イデアルとする。
(5.1) O_Lpは、O_Lp=q_1^(e_1)...q_g^(e_g)
の形にあらわされる。
q_1,...,q_gはO_Lの相異なる0でない素イデアル、e_i≧1
e_1=...=^(e_g)=1であるとき、pはLにおいて不分岐(unramified)であるという。不分岐でないとき、すなわちあるiについてe_i≧2であるとき、
pはLにおいて分岐(ramified)であるという。
例えば、K=Q,L=Q(√(-1))
のとき、Lにおいて分岐するZの0でない素イデアルは2Zのみである。
一般に(5.1)について、
(5.2) ?[i=1,g] e_i ≦ [L:K]
([L:K]は体の拡大次数)であること、したがって、とくにg≦[L:K]であることが
しられている。
定義5.3
O_Lpが、[L:K]個のO_Lの相異なる0でない素イデアルの積となるとき、すなわちg=[L:K] であるとき、pはLにおいて完全分解するという。
完全分解すれば不分岐である。
-------------------------------
--------------------------
pが4でわると1余る素数pなら、
p=x^2+y^2
となる自然数x,yが存在する。
たとえば、4でわると1余る素数5,13,17については、
5=2^2+1^2,
13=3^2+2^2,
17=4^2+1^2
しかし、4でわると3余る素数pについては、
p=x^2+y^2
となる有理数x,yさえ存在しない。
複素数i=√(-1)を用いて考えると、
5=2^2+1^2=(2+i)(2-i)
13=3^2+2^2=(3+2i)(3-2i)
17=4^2+1^2=(4+i)(4-i)
のように、4でわると1余る素数が
Z[i]={a+bi; a,b ∈Z} {Zは整数全体の集合}
の中で積の形にわかれないという素数(prime number)としての性質を失い、
積のかたちに分解することと関係している。
ここにあらわれた2+i,2-i,3+2iなどは、Zにおける素数にあたる
Z[i]の素元(prime element)である。
p=x^2+y^2
となる自然数x,yが存在する。
たとえば、4でわると1余る素数5,13,17については、
5=2^2+1^2,
13=3^2+2^2,
17=4^2+1^2
しかし、4でわると3余る素数pについては、
p=x^2+y^2
となる有理数x,yさえ存在しない。
複素数i=√(-1)を用いて考えると、
5=2^2+1^2=(2+i)(2-i)
13=3^2+2^2=(3+2i)(3-2i)
17=4^2+1^2=(4+i)(4-i)
のように、4でわると1余る素数が
Z[i]={a+bi; a,b ∈Z} {Zは整数全体の集合}
の中で積の形にわかれないという素数(prime number)としての性質を失い、
積のかたちに分解することと関係している。
ここにあらわれた2+i,2-i,3+2iなどは、Zにおける素数にあたる
Z[i]の素元(prime element)である。
- mixiユーザー
- ログインしてコメントしよう!
|
|
|
|
独学ノート(土筆の子) 更新情報
-
最新のイベント
-
まだ何もありません
-
-
最新のアンケート
-
まだ何もありません
-